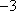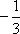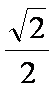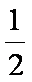- 两角和与差的正切函数
- 共28题
E,F是等腰直角△ABC斜边AB上的三等分点,则
正确答案
解析
略
解法1:约定AB=6,AC=BC=


解得
解法2:坐标化。约定AB=6,AC=BC=


知识点
已知向量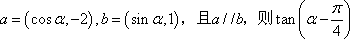
正确答案
解析
略
知识点
某兴趣小组测量电视塔AE的高度H(单位:m),如示意图,垂直放置的标杆BC的高度h=4m,仰角∠ABE=

(1)该小组已经测得一组



(2)该小组分析若干测得的数据后,认为适当调整标杆到电视塔的距离d(单位:m),使



正确答案
(1)124m.
(2)
解析
(1)


AD—AB=DB,故得

因此,算出的电视塔的高度H是124m。
(2)由题设知



故当

因为




故所求的

知识点
在ABC中,若tanAtanB= tanA+ tanB+ 1,则cosC的值是
正确答案
解析
由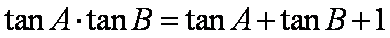
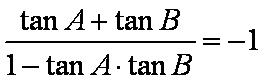
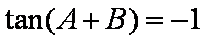
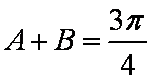
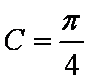
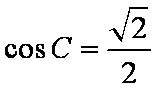
知识点
12.如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α、β,它们的终边分别交单位圆于A、B两点.已知A、B两点的横坐标分别是

正确答案
﹣3
解析
∵cosα=

∴sinα=



∴tanα=7,tanβ=
∴tan(α+β)=

故答案为:﹣3.
知识点
9.已知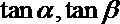
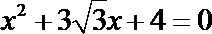
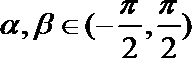
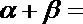
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 如图,在平面直角坐标系





(1)求
(2)求
正确答案
(1)由已知得:
∵
∴
∴ 
∴
(2)∵
∴

∴
∴
解析
解析已在路上飞奔,马上就到!
知识点
17.在

(1)求证:
(2)若tanC=2,求A的值。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知
(1)求
(2)求
正确答案

(1)
(2)
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析