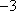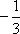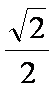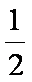- 两角和与差的正切函数
- 共28题
1
题型:
单选题
|
E,F是等腰直角△ABC斜边AB上的三等分点,则
正确答案
D
解析
略
解法1:约定AB=6,AC=BC=


解得
解法2:坐标化。约定AB=6,AC=BC=


知识点
两角和与差的正切函数
1
题型:
单选题
|
已知向量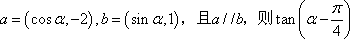
正确答案
B
解析
略
知识点
三角函数的恒等变换及化简求值两角和与差的正切函数平面向量共线(平行)的坐标表示
1
题型:简答题
|
某兴趣小组测量电视塔AE的高度H(单位:m),如示意图,垂直放置的标杆BC的高度h=4m,仰角∠ABE=

(1)该小组已经测得一组



(2)该小组分析若干测得的数据后,认为适当调整标杆到电视塔的距离d(单位:m),使



正确答案
(1)124m.
(2)
解析
(1)


AD—AB=DB,故得

因此,算出的电视塔的高度H是124m。
(2)由题设知



故当

因为




故所求的

知识点
两角和与差的正切函数解三角形的实际应用利用基本不等式求最值
1
题型:
单选题
|
在ABC中,若tanAtanB= tanA+ tanB+ 1,则cosC的值是
正确答案
B
解析
由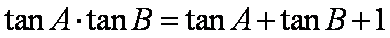
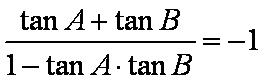
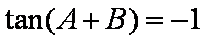
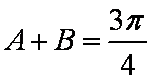
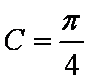
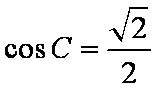
知识点
同角三角函数间的基本关系诱导公式的作用两角和与差的正切函数
1
题型:简答题
|
17.在

(1)求证:
(2)若tanC=2,求A的值。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
两角和与差的正切函数正弦定理平面向量数量积的运算
下一知识点 : 二倍角的正弦
扫码查看完整答案与解析