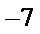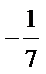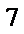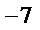- 两角和与差的正切函数
- 共28题
1
题型：
单选题
|
6．当
A
B
C
D
正确答案
A
解析
解析已在路上飞奔，马上就到！
知识点
正切函数的值域弦切互化两角和与差的正切函数
1
题型：填空题
|
11．已知锐角A，B满足tan（A＋B）＝2tanA，则tanB的最大值是（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
正切函数的单调性两角和与差的正切函数角的变换、收缩变换
1
题型：
单选题
|
4.函数y=sin（πx+φ）（φ>0）的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,则tan∠APB=（ ）.
A10
B8
C
D
正确答案
B
解析
根据题意过点P作PE
知识点
由y=Asin（ωx+φ）的部分图象确定其解析式两角和与差的正切函数
1
题型：
单选题
|
2．若复数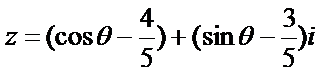
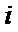
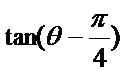
A
B
C
D
正确答案
A
解析
由题意得，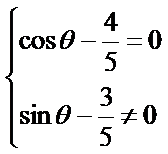
所以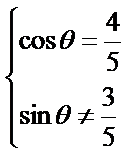
所以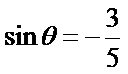
所以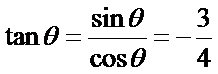
所以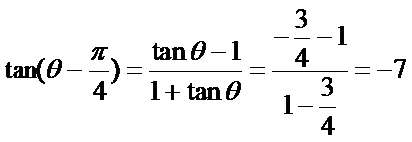
故选A。
考查方向
本题主要考查复数的概念、同角三角函数的基本关系、两角和与差的三角函数等知识，意在考查考生的运算能力和逻辑推理能力。
解题思路
1.先根据条件求出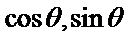
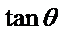
2.根据两角差的正切公式求出
易错点
对于纯虚数的概念理解不好，不注意虚部不为0，导致误选D；
知识点
三角函数的化简求值两角和与差的正切函数复数的基本概念
1
题型：
单选题
|
7.已知向量
A3
B﹣3
C
D
正确答案
B
解析
所以
所以tanα=
tan（α﹣
考查方向
共线向量的坐标表示及两角差的正切公式.
解题思路
本题考查了共线向量的坐标表示及两角差的正切公式.先算出tanα的值，带入两角差的正切公式即可。
易错点
本题易在向量的平行的坐标表示中出错
知识点
两角和与差的正切函数平行向量与共线向量
下一知识点 : 二倍角的正弦
扫码查看完整答案与解析