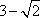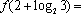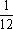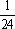- 函数的基本性质
- 共1471题
已知点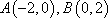
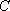
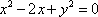
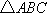
正确答案
解析
略
知识点
设定义在R上的函数
正确答案
解析
略
知识点
如果函数
A
B
C
D
正确答案
解析
略
知识点
已知变量
正确答案
9
解析
略
知识点
设命题p：函数
正确答案
见解析
解析
p：
q：
∵“p且q”为假命题 ∴p,q至少有一假
（1）若p真q假，则
（2）若p假q真，则
（3）若p假q假，则
∴
知识点
为了在夏季降温和冬季供暖时减少能源损耗，房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层，每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C（单位：万元）与隔热层厚度x（单位：cm）满足关系：
（1）求k的值及
（2）隔热层修建多厚时，总费用
正确答案
见解析
解析
（1）设陋热层厚度为
由题设，每年能源消耗费用为
再由
而建造费用为
最后得隔热层建造费用与20年的能源消耗费用之和为
（2）
解得
当
对应的最小值为
当隔热层修建5cm厚时，总费用达到最小值70万元. ………………………………………………12分
知识点
正确答案
0
解析
展开式的第r＋1项为
知识点
已知函数
正确答案
解析
略
知识点
已知函数
A-
B-e
Ce
D
正确答案
解析
略
知识点
已知函数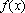
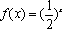
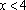
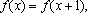
A
B
C
D
正确答案
解析
略
知识点
扫码查看完整答案与解析