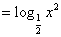- 函数的基本性质
- 共1471题
已知函数
（1）当
（2）求
正确答案
见解析
解析
（1）解：当
由 
（2）解：
① 当
所以
当
② 当
故
③ 当
所以
综上，
知识点
若直线
Aa2+b2≤1
Ba2+b2≥1
C
D
正确答案
解析
由题意可得（bcosα+asinα）2=a2b2，再利用 （bcosα+asinα）2≤（a2+b2）•（cos2α+sin2α），化简可得
解：若直线
∴bcosα+asinα=ab，∴（bcosα+asinα）2=a2b2。
∵（bcosα+asinα）2≤（a2+b2）•（cos2α+sin2α）=（a2+b2），
∴a2b2≤（a2+b2），∴
故选D。
知识点
.如图2，某简单几何体的正（主）视图与侧（左）视图都是边长为1的正方形，且其体积为
A
B
C
D
正确答案
解析
知识点
下列函数中既是奇函数，又在（0，+∞）上单调递增的是（ ）
正确答案
解析
解：由于函数y=x2是偶函数，故不满足条件。
由于函数y=x3是奇函数，且在（0，+∞）上单调递增，故满足条件。
由于函数y=﹣x是奇函数，但在（0，+∞）上单调递减，故不满足条件。
由于函数 y=tanx是奇函数，故不满足条件。
故选B。
知识点
下列四个函数中，既是奇函数又在定义域上单调递增的是（）
A
B
C
D
正确答案
解析
略
知识点
已知函数
A
B
C
D
正确答案
解析
略
知识点
已知函数
（1）求
（2）求函数
正确答案
（1）
（2）
解析
（1）
（2）由
因为
所以
因为函数
由
得
所以
………………………………13分
知识点
函数f（x）=x|x+a|+b是奇函数的充要条件是（ ）
A
B
C
D
正确答案
解析
若f（x）是奇函数，则f（-x）=-f（x），即﹣x|x﹣a|+b=﹣x|x+a|﹣b恒成立，
亦即x（|x﹣a|﹣|x+a|）=2b恒成立，
要使上式恒成立，只需|x﹣a|﹣|x+a|=2b=0，即a=b=0，
故函数f（x）=x|x+a|+b是奇函数的充要条件是a=b=0，
故选C。
知识点
下列函数中，既是偶函数又在（0，＋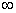
Ay＝cosx
By＝x3
Cy
Dy=
正确答案
解析
略
知识点
“
正确答案
解析
知识点
扫码查看完整答案与解析