- 函数的基本性质
- 共1471题
在平面直角坐标系xOy中,“直线


“ ”。
正确答案
解析
易得


知识点
设函数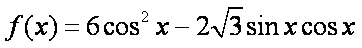
(1)求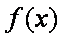
(2)在锐角△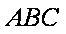
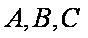
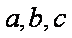
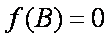
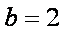
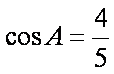
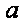
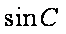
正确答案
见解析。
解析
(1)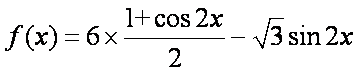
=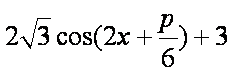
所以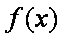
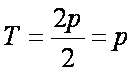
值域为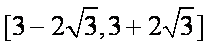
(2)由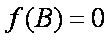
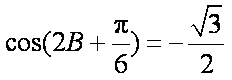
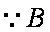
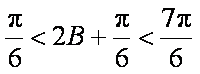
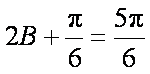
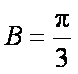
∵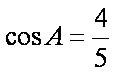
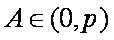
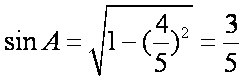
在△ABC中,由正弦定理得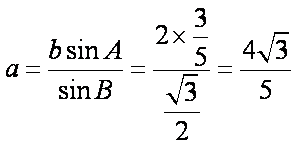
∴
知识点
已知函数
(1)求
(2)若函数






正确答案
(1)

解析
解析:(1)因为

所以函数













当




知识点
设

数列{an}的首项a1=1,前n项和为Sn,对于任意的正整数n,an+Sn=
(1)若k=0,求证:数列{an}是等比数列;
(2)试确定所有的自然数k,使得数列{an}能成等差数列。
正确答案
见解析
解析
(1)若


当


当


①

若



故数列

(2)(ⅰ)若
(ⅱ)若

当

当


③-④得 
要使数列{an}是公差为d(d为常数)的等差数列,必须有
而


故当



(ⅲ) 若

当


⑤-⑥得 
要使数列



且
考虑到a1=1,所以
故当

此时
(ⅳ)当







综上得,当且仅当


知识点
函数
正确答案
解析
函数
知识点
设函数
(1)若a=b=1,求f3(x)在[0,2]上的最大值和最小值;
(2)若对任意x1,x2∈[﹣1,1],都有|f3(x1)﹣f3(x2)|≤1,求a的取值范围;
(3)若|f4(x)|在[﹣1,1]上的最大值为
正确答案
见解析。
解析
(1)由
则
在(0,1)内,

所以在(0,1)内,

则f3(x)的极大值为f3(1)=3,由f3(0)=1,
所以函数
(2)因为对任意x1,x2∈[﹣1,1],都有|f3(x1)﹣f3(x2)|≤1,
所以|f3(1)﹣f3(﹣1)|≤1,从而有|(﹣1+3a+b)﹣(1﹣3a+b)|=|6a﹣2|≤1,
所以
又
在
所以f3(x)在
f3(x)在
只需
即

所以a的取值范围是
(3)
由f4(x)在[﹣1,1]上的最大值为

所以



①+②得,



将

将

所以a=0。
综上知a,b的值分别为0,
知识点
若圆C:x2+y2+2x-4y+3=0,关于直线2ax+by+6=0对称 ,则由点(a,b)向圆所作的切线长的最小值为
正确答案
4
解析

















知识点
观察下列等式
1=1
2+3+4=9
3+4+5+6+7=25
4+5+6+7+8+9+10=49
……
照此规律,第n个等式为 。
正确答案
n+(n+1)+(n+2)+…+(3n-2)=(2n-1)2
解析
等式左边为的第一个数为对应行数,每行的整数个数为奇数个,等式右边为对应奇数个的平方,所以通项公式为n+(n+1)+(n+2)+…+(3n-2)=(2n-1)2。
知识点
已知平面向量






正确答案
答案:
解析
略
知识点
设集合


正确答案
解析
略
知识点
扫码查看完整答案与解析