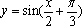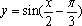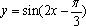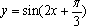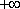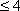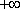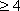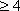函数的基本性质
共1471题

函数的基本性质
共1471题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

下列四个函数中，最小正周期为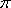，且图象关于直线对称的是（）

正确答案

解析

略

知识点

函数的单调性及单调区间

题型：单选题

单选题 · 5 分

设f（x）与g（x）是定义在同一区间[a，b]上的两个函数，若函数y=f（x）﹣g（x）在x∈[a，b]上有两个不同的零点，则称f（x）和g（x）在[a，b]上是“关联函数”，区间[a，b]称为“关联区间”，若f（x）=x2﹣3x+4与g（x）=2x+m在[0，3]上是“关联函数”，则m的取值范围为（　　）

正确答案

解析

∵f（x）=x2﹣3x+4与g（x）=2x+m在[0，3]上是“关联函数”，

故函数y=h（x）=f（x）﹣g（x）=x2﹣5x+4﹣m在[0，3]上有两个不同的零点，

故有，即

解得﹣＜m≤﹣2，

故选A。

知识点

函数的单调性及单调区间

题型：单选题

单选题 · 5 分

如果函数y=f(x)图像上任意一点的坐标（x,y）都满足方程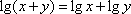，那么正确的选项是（）

Ay=f(x)是区间（0，）上的减函数，且x+y

By=f(x)是区间（1，）上的增函数，且x+y

Cy=f(x)是区间（1，）上的减函数，且x+y

Dy=f(x)是区间（1，）上的减函数，且x+y

正确答案

解析

略

知识点

函数的单调性及单调区间

题型：简答题

简答题 · 13 分

已知函数的最小正周期为，且图象过点.

（1）求的值；

（2）设，求函数的单调递增区间.

正确答案

（1）2；

（2）

解析

（1）由最小正周期为可知 ………………2分

由得，

又，

所以， ………………5分

（2）由（1）知

所以……………………9分

解

得………………………12分

所以函数的单调增区间为.………………………13分

知识点

函数的单调性及单调区间

题型：填空题

填空题 · 5 分

如图，圆的直径，直线与圆O相切于点，于D，

若，设，则______。

正确答案

解析

略

知识点

函数的单调性及单调区间

题型：简答题

简答题 · 14 分

已知函数（），是自然对数的底数。

（1）试判断函数在区间上的单调性；

（2）当，时，求整数的值，使得函数在区间（）上存在零点；

（3）若存在，[－1，1]，使得，求的取值范围。

正确答案

见解析。

解析

已知函数，是自然对数的底数。

（1）试判断函数在区间上的单调性；

（2）当，时，求整数的值，使得函数在区间上存在零点；

（3）若存在，使得，试求的取值范围。

（1）

由于，故当时，，所以，

故函数在上单调递增 .

（2），，

，

当时，，，故是上的增函数；

同理，是上的减函数.

，当，，

故当时，函数的零点在内，满足条件；

，当，，

故当时，函数的零点在内，满足条件.

综上所述或.

（3），

因为存在，使得，所以当时，

，

①当时，由，可知，，∴；

②当时，由，可知，，∴；

③当时，.

∴在上递减，在上递增，

∴当时，，

而，

设，因为（当时取等号），

∴在上单调递增，而，

∴当时，，

∴，

∴，即，

设，则

∴函数在上为增函数，

∴.

即的取值范围是…

知识点

函数的单调性及单调区间

题型：填空题

填空题 · 5 分

在给定的函数中：① ；②；③；④，既是奇函数又在定义域内为减函数的是 .

正确答案

①

解析

略

解题思路

略

知识点

函数的单调性及单调区间

题型：单选题

单选题 · 5 分

下列函数在其定义域是增函数的是

正确答案

解析

只在其周期内单调递增，在上单调递减，在上单调递增，在上单调递减，在上单调递增；

知识点

函数的单调性及单调区间

题型：填空题

填空题 · 4 分

函数的单调递减区间是____________。

正确答案

解析

略

知识点

函数的单调性及单调区间

题型：简答题

简答题 · 13 分

已知函数.

（1）求的单调区间；

（2）是否存在实数，使得对任意的，都有？若存在，求的取值范围；若不存在，请说明理由。

正确答案

见解析

解析

（1）的定义域为. .…………………2分

当时，在区间上，. 所以的单调递减区间是.……………3分

当时，令得或（舍）。

函数,随的变化如下：

所以的单调递增区间是，单调递减区间是. ……………6分

综上所述，当时，的单调递减区间是；

当时，的单调递增区间是，单调递减区间是.

（2）由（1）可知：

当时, 在上单调递减。

所以在上的最大值为，即对任意的，都有.……7分

当时，

① 当，即时，在上单调递减.

所以在上的最大值为，即对任意的，都有.………10分

② 当，即时，在上单调递增，

所以 .又，

所以，与对于任意的，都有矛盾. ………………………12分

综上所述，存在实数满足题意，此时的取值范围是.………………………13

知识点

函数的单调性及单调区间

继续学习学习下一知识点

下一知识点 : 二次函数与幂函数

百度题库 > 高考 > 文科数学 > 函数的基本性质

扫码查看完整答案与解析