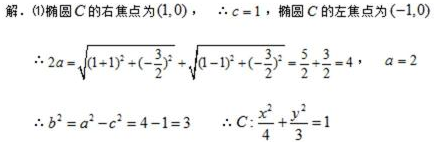- 函数的基本性质
- 共1471题
22.已知直线




求(Ⅰ)求直线
(Ⅱ)设

正确答案
(Ⅱ)方法一:
由
得
设
当



于是,


故
要使
∴ a的取值范围为
方法二:由(Ⅰ)知,
∴






故


故

要使解得
只需
(ii)若




故不可能
综上所述,
解析
解析已在路上飞奔,马上就到!
知识点
17.在平面直角坐标系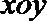

(1)求向量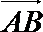
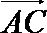
(2)若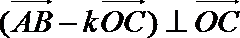
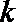
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.幂函数f(x)=x
正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数


(1)求

(2)已知定点




(3)当

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知点
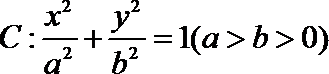

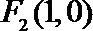
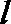
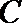
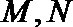
(1)求椭圆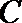
(2)若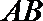
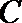
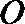
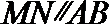
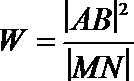


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 已知函数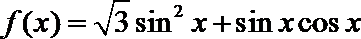
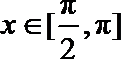
(Ⅰ)求方程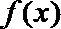
(Ⅱ)求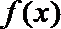
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数

(1)求
(2)若
正确答案
(1)
由已知得
解得
(2)由已知只须
令





令





在
则
由
解得
解析
解析已在路上飞奔,马上就到!
知识点
21.有一种变压器铁芯的截面呈如图所示的正十字形,为保证所需的磁通量,要求正十字形的面积为4
正确答案
设外接圆半径为R,AB =x(0<x<R),DG =y,则4R2=x2+y2 (1),
由已知条件有2xy-x2=4

代入(1)得4R2= x2 +
∴4R2=

当且仅当
代入(2)得y=1+
∴当 x=2 且y=1+
此时正十字形外接圆周长最短。
答:正十字形的长和宽分别为(1+
解析
解析已在路上飞奔,马上就到!
知识点
14.已知函数











正确答案
b>a>c
解析
解析已在路上飞奔,马上就到!
知识点
8.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析