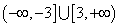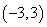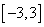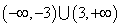函数的基本性质
共1471题

函数的基本性质
共1471题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 12 分

已知函数，

（1）求函数的周期及单调递增区间；

（2）在中，三内角，，的对边分别为，已知函数的图象经过点成等差数列，且，求的值.

正确答案

见解析。

解析

………………………………………………3分

（1）最小正周期：， ………………………………………………4分

由可解得：

，

所以的单调递增区间为：; ………………6分

（2）由可得：

所以, ………………………………………………8分

又因为成等差数列，所以， ………………9分

而 ………………………………10分

，

. ………………………………………………12分

知识点

函数单调性的判断与证明

题型：单选题

单选题 · 5 分

函数的定义域是（）

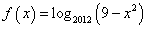
正确答案

解析

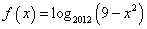
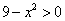
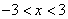
要使函数有意义，需使，解得。

知识点

函数单调性的判断与证明

题型：单选题

单选题 · 5 分

如图，在圆的内接三角形中，，，则等于（）。

A13

正确答案

解析

略

知识点

函数单调性的判断与证明

题型：单选题

单选题 · 5 分

函数的图像大致是（）

正确答案

解析

略

知识点

函数单调性的判断与证明

题型：简答题

简答题 · 12 分

已知是偶函数，且在上单调递减，对任意,都有。

（1）指出在上的单调性（不要求证明），并求的值；

（2）为常数，，解关于的不等式。

正确答案

见解析。

解析

（1）在上是增函数，

，

（2）因为是偶函数，所以，

不等式即为，在上递增，

，。

∵，，

①若，则，不等式解集为；

②若，则不等式解集为；

③若，则不等式解集为，

知识点

函数单调性的判断与证明函数奇偶性的性质其它不等式的解法

题型：填空题

填空题 · 5 分

在一次选秀比赛中，五位评委为一位表演者打分，若去掉一个最低分后平均分为90分，去掉一个最高分后平均分为86分.那么最高分比最低分高（）分。

正确答案

解析

略

知识点

函数单调性的判断与证明

题型：简答题

简答题 · 13 分

已知函数

（1）求的值；

（2）求函数的单调增区间与最大值。

正确答案

（1）1

解析

（1）...................4分

（2） ...................2分

.....................3分

令....................5分

，

所以函数的单调增区间是................7分

时，的最大值为................9分

知识点

函数单调性的判断与证明

题型：简答题

简答题 · 12 分

全国第十二届全国人民代表大会第二次会议和政协第十二届全国委员会第二次会议，2014年3月在北京开幕，期间为了了解国企员工的工资收入状况，从108名相关人员中用分层抽样方法抽取若干人组成调研小组，有关数据见下表：（单位：人）

（1）求，；

（2）若从中层、高管抽取的人员中选人，求这二人都来自中层的概率。

正确答案

见解析。

解析

（1）由题意可得，所以，. ……………………3分

（2）记从中层抽取的人为，，，从高管抽取的人为，，

则抽取的人中选人的基本事件有：，，，，，，，，，共种。 ……8分

设选中的人都来自中层的事件为，

则包含的基本事件有：，，共种. ………………10分

因此.

故选中的人都来自中层的概率为. ……………………………………12分

知识点

函数单调性的判断与证明

题型：单选题

单选题 · 5 分

变量、满足线性约束条件，则目标函数，仅在点取得最小值，则的取值范围是

正确答案

解析

略

知识点

函数单调性的判断与证明

题型：单选题

单选题 · 5 分

设函数在上有定义，对于任一给定的正数，定义函数，则称函数为的“界函数”，若给定函数，则下列结论不成立的是

正确答案

解析

略

知识点

函数单调性的判断与证明

继续学习学习下一知识点

下一知识点 : 二次函数与幂函数

百度题库 > 高考 > 文科数学 > 函数的基本性质

扫码查看完整答案与解析