充要条件的判定
共176题

· 充要条件的判定

充要条件的判定
共176题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

设a＞0 a≠1 ，则“函数f(x)= ax在R上是减函数 ”，是“函数g(x)=(2-a) 在R上是增函数”的

A充分不必要条件

B必要不充分条件

C充分必要条件

D既不充分也不必要条件

正确答案

解析

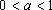
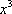
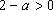
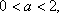
p：“函数f(x)= ax在R上是减函数 ”等价于；q：“函数g(x)=(2-a) 在R上是增函数”等价于，即且a≠1，故p是q成立的充分不必要条件. 答案选A。

知识点

充要条件的判定函数单调性的性质

题型：单选题

单选题 · 5 分

设，则的最小值是

正确答案

解析

＝

≥0＋2＋2＝4

当且仅当a－5c＝0,ab＝1,a(a－b)＝1时等号成立

如取a＝,b＝,c＝满足条件。

知识点

充要条件的判定

题型：单选题

单选题 · 5 分

“”是“”的

A充分而不必要条件

B必要而不充分条件

C充要条件

D既不充分也不必要条件

正确答案

解析

，故“”是“”的充分而不必要条件

知识点

充要条件的判定

题型：简答题

简答题 · 12 分

已知数列的各项均为正数，记，，，

（1）若，且对任意，三个数组成等差数列，求数列的通项公式.

（2）证明：数列是公比为的等比数列的充分必要条件是：对任意，三个数组成公比为的等比数列.

正确答案

见解析

解析

（1）对任意,三个数是等差数列，所以

即亦即故数列是首项为１，公差为４的等差数列.于是

（2）①必要性：若数列是公比为ｑ的等比数列，则对任意，有

由知，均大于０，于是

即＝＝，所以三个数组成公比为的等比数列.

②充分性：若对于任意，三个数组成公比为的等比数列，

则，

于是得

即

由有即，从而.

因为，所以，故数列是首项为，公比为的等比数列，

综上所述，数列是公比为的等比数列的充分必要条件是：对任意n∈N﹡，三个数组成公比为的等比数列.

知识点

充要条件的判定等差数列的性质及应用等比数列的判断与证明

题型：单选题

单选题 · 5 分

已知是三个相互平行的平面,平面之间的距离为,平面之间的距离为.直线与分别交于.那么是的 ( )

A充分不必要条件

B必要不充分条件

C充分必要条件

D既不充分也不必要条件

正确答案

解析

平面平行，由图可以得知：

如果平面距离相等，根据两个三角形全等可知

如果，同样是根据两个三角形全等可知

知识点

充要条件的判定

继续学习学习下一知识点

下一知识点 : 充要条件的应用

百度题库 > 高考 > 理科数学 > 充要条件的判定

扫码查看完整答案与解析