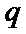- 充要条件的判定
- 共176题
3.设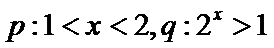
A充分不必要条件
B必要不充分条件
C充
D既不充分也不必要条件
正确答案
解析
由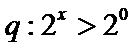
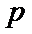
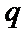
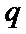
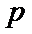
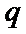
考查方向
解题思路
先利用指数函数的运算法则，然后判断是什么样的条件。
易错点
充分条件和必要条件混淆
知识点
7．设p：实数x，y满足(x–1)2–(y–1)2≤2，q：实数x，y满足
正确答案
解析
画出可行域，可知命题q中不等式组表示的平面区域
考查方向
解题思路
本题考查充分性与必要性的判断问题，首先是分清条件和结论，然后考察条件推结论，结论推条件是否成立.这类问题往往与函数、三角、不等式等数学知识结合起来考，本题条件与
易错点
本题考查充分性与必要性的判断问题，条件和结论的区分上易混淆。
知识点
15．在平面直角坐标系中，当P(x，y)不是原点时，定义P的“伴随点”为
当P是原点时，定义P的“伴随点“为它自身，平面曲线C上所有点的“伴随点”所构成的曲线
①若点A的“伴随点”是点
②单位圆的“伴随曲线”是它自身；
③若曲线C关于x轴对称，则其“伴随曲线”
④一条直线的“伴随曲线”是一条直线.
其中的真命题是_____________（写出所有真命题的序列）.
正确答案
②③
解析
① 设
随点分别是
考查方向
解题思路
本题考查新定义问题，属于创新题，符合新高考的走向．它考查学生的阅读理解能力，接受新思维的能力，考查学生分析问题与解决问题的能力，新定义的概念实质上只是一个载体，解决新问题时，只要通过这个载体把问题转化为我们已经熟悉的知识即可．本题新概念“伴随”实质是一个变换，一个坐标变换，只要根据这个变换得出新的点的坐标，然后判断，问题就得以解决．
易错点
本题考查新定义问题，属于创新题，易在定义的分析和对称性的应用中出错。
知识点
3.在
正确答案
解析
∵在
∴
∴所以选项A为正确选项
考查方向
解题思路
在
易错点
本题易在充分必要条件的判定混淆使用
知识点
6.已知直线a，b分别在两个不同的平面α，β内.则“直线a和直线b相交”是“平面α和平面β相交”的
正确答案
解析
直线a与直线b相交,则
考查方向
解题思路
根据充分条件与必要条件的判定推理,可结合周边事物举例分析.
易错点
注意立体几何中线面关系的分析,可结合周边事物推理分析.
知识点
扫码查看完整答案与解析