- 充要条件的判定
- 共176题
3.
正确答案
解析
若

考查方向
充要条件的判断
三角形的性质
解题思路
根据选项结合钝角三角形的性质判断
易错点
对三角形的性质掌握不牢固
知识点
2.已知


正确答案
解析
由题意可知,第一个命题是第二个命题的充分不必要题哦啊间,所以选A
考查方向
必要条件、充分条件与充要条件判断
解题思路
根据复数的性质和特征,解出m的值,即可判断结论
易错点
对复数的概念理解不透彻
知识点
城市房屋白蚁防治中,通过在白蚁蛀食的食物中或在白蚁主要出入的蚁路中喷入白蚁药物,使出入的白蚁身体粘上白蚁药粉,药粉通过相互传染传递给其他白蚁,导致整巢白蚁中毒死亡的办法称之为( )。
A.药杀法
B.挖巢法
C.诱杀法
D.生物防治法
正确答案
A
解析
暂无解析
7. 直线




则“


(填写“充分不必要”、“必要不充分”、“充要”、“既不充分又不必要”之一)
正确答案
充分而不必要
解析
由直线






考查方向
充分条件、必要条件、充要条件的判断
解题思路
根据题意和相关性质,分别求出两个命题,然后进行判断
易错点
化简错误
知识点
3.对于函数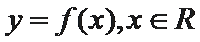
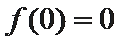
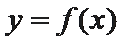
正确答案
解析
一个定义在R上的函数,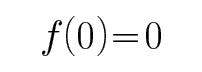
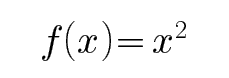
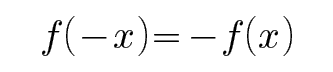
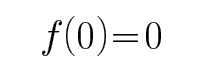
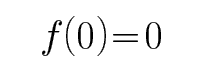
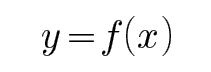
考查方向
1.充分,必要条件的判断;2.奇函数的性质。
解题思路
判断两者能否互相推导。
易错点
不注意函数的定义域,奇函数的定义理解错误也容易出错。
教师点评
难度不大,举出特例就能解决。
知识点
3.“函数


正确答案
解析
函数f(x)=kx-3在[-1,1]上有零点⇔f(-1)f(1)≤0,
∴(-k-3)(k-3)≤0,解得k≥0,或k≤-3.
∴“函数f(x)=kx-3在[-1,1]上有零点”是“k≥3”的必要不充分条件.
故选:B
考查方向
必要条件、充分条件与充要条件的判断
函数零点的判断
解题思路
函数f(x)=kx-3在[-1,1]上有零点⇔f(-1)f(1)≤0,解出即可判断出结论
易错点
逻辑关系混乱,不会判断函数有无零点
教师点评
此题考察简易逻辑中命题与命题之间的关系,属于基础题,一般结合不等式,平面与直线等知识点一同考察
知识点
5.设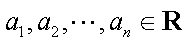
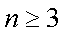
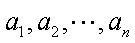
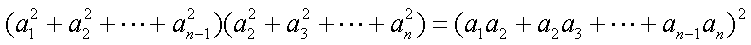
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.“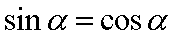
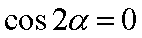
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. “

正确答案
解析
因为





考查方向
解题思路
分别从充分性和必要性证明。
易错点
充分性和必要性概念理解清楚。
知识点
21. 正数数列







差中项,


(1)若



(2)求证:

充分性和必要性的证明。
(3)记




正确答案



解析
正整数数列






















所以


即







对一切




差中项,












考查方向
解题思路
根据对一切
























对一切








可得

易错点
计算要仔细准确。
①不容易考虑到基本不等式②利用单调性比较大小在数列中的应用。
知识点
扫码查看完整答案与解析








