- 充要条件的应用
- 共64题
下列有关命题的叙述错误的 ( )
正确答案
解析
略。
知识点
已知






正确答案
解析
略
知识点
设平面






正确答案
解析
略
知识点
已知
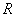
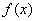
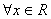

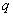
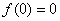
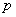
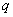
正确答案
解析
略
知识点
“

正确答案
解析
略
知识点
已知数列



(1)若



(2)证明:数列




正确答案
见解析
解析
(1)因为对任意

所以
所以
即
所以数列
所以
(2)(1)充分性:若对于任意



所以
即
因为当


所以
因为
所以
即数列


(2)必要性:若数列



因为
所以



即




………13分
综上所述,数列



知识点
若


正确答案
解析
当













知识点
“

正确答案
解析
略
知识点
在数列






(1)若数列





(2)证明:一个等比数列为


(3)若











正确答案
见解析
解析
(1)由




于是
所有满足条件的数列





(2)(必要性)设数列









所以


(充分性)若一个等比数列



以

若一个等比数列



所以

(3)因



所以数列


假设存在正整数

切
当



下面证明:

由于
所以
------------------5分
知识点
关于x的不等式ax2-2x+1<0的解集非空的一个必要不充分条件是( )
正确答案
解析
因为ax2-2x+1<0的解集非空,显然a≤0成立,由解得0<a<1.综上知ax2-2x+1<0的解集非空的充要条件为a<1,因为{a|a<1}⊂{a|a≤1},故选B.
知识点
扫码查看完整答案与解析














