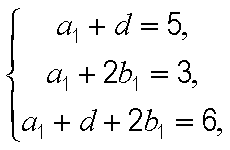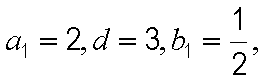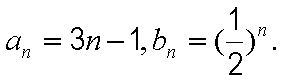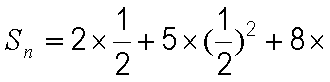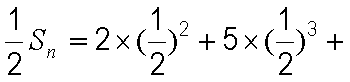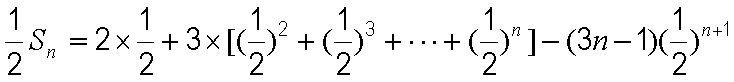- 二次函数在闭区间上的最值
- 共44题
过直线y=﹣1上的动点A(a,﹣1)作抛物线y=x2的两切线AP,AQ,P,Q为切点。
(1)若切线AP,AQ的斜率分别为k1,k2,求证:k1•k2为定值。
(2)求证:直线PQ过定点。
正确答案
见解析
解析
解:(1)设过A作抛物线y=x2的切线的斜率为k,
则切线的方程为y+1=k(x﹣a),
与方程y=x2联立,消去y,得x2﹣kx+ak+1=0。
因为直线与抛物线相切,所以△=k2﹣4(ak+1)=0,
即k2﹣4ak﹣4=0.由题意知,此方程两根为k1,k2,
∴k1k2=﹣4(定值),
(2)设P(x1,y1),Q(x2,y2),由y=x2,得y′=2x。
所以在P点处的切线斜率为:
因此,切线方程为:y﹣y1=2x1(x﹣x1)。
由y1=x12,化简可得,2x1x﹣y﹣y1=0。
同理,得在点Q处的切线方程为2x2x﹣y﹣y2=0。
因为两切线的交点为A(a,﹣1),故2x1a﹣y1+1=0,2x2a﹣y2+1=0。
∴P,Q两点在直线2ax﹣y+1=0上,即直线PQ的方程为:2ax﹣y+1=0。
当x=0时,y=1,所以直线PQ经过定点(0,1)
知识点
已知函数
(1)若


(2)若函数

(3)设函数




正确答案
见解析
解析
解析:(1)当










(2)
















(3)∵






①当

















②当






③当













知识点
已知极坐标的极点在平面直角坐标系的原点





(1)求点
(2)求点

正确答案
见解析
解析
(1)

所以点
(2)因为

所以


法一:由(1)点





法二:





知识点
某几何体的三视图如右图所示,已知其正视图的周长为6,则该几何体体积的最大值为
正确答案
解析
由三视图可知,这个几何体为圆柱,设圆柱的底面半径为r,高为h,则h+2r=3,圆柱的体积为:
V(r)=Sh=





当r




r=1是V(r)的一个唯一的极大值点,也是最大值点,所以,
r=1时,圆柱体积的最大值为:V=
知识点
等差数列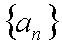
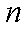
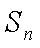
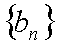
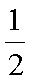
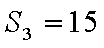
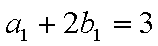
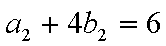
(1)求数列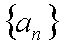
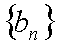
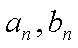
(2)求数列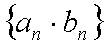
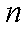
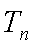
正确答案
见解析
解析
解析:
(1)设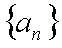
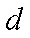
所以
解得
所以
(2)由(1)知
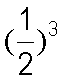
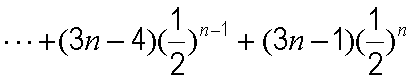
①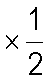
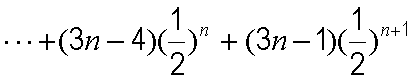
①-②得
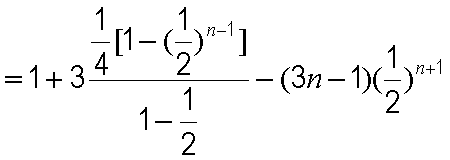
整理得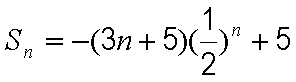
知识点
扫码查看完整答案与解析