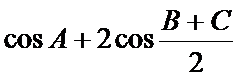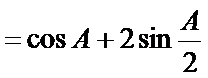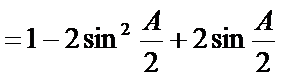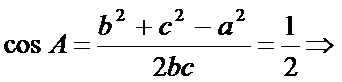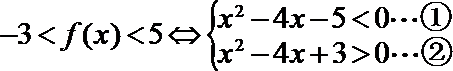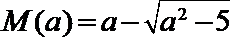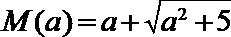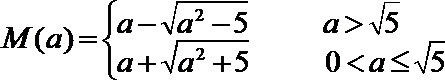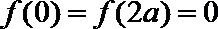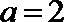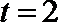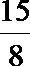- 二次函数在闭区间上的最值
- 共44题
21.已知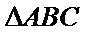
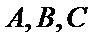
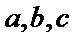
(1)若当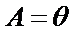
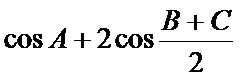

(2)设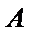
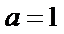
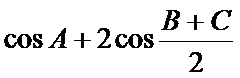
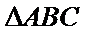
正确答案
(1)因为
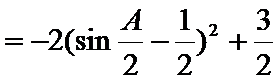
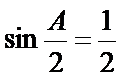
即三角形的内角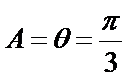
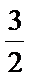
(2)由(1)结论可得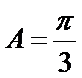
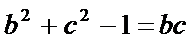
又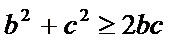

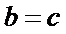
所以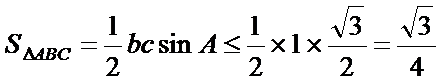
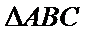

解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数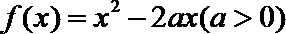
(1)当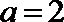
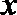
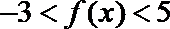
(2)对于给定的正数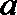



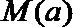
(3)函数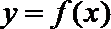
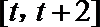

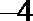
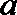
正确答案
(1)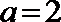
由①得,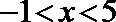
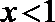
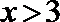
∴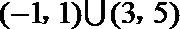
(2)∵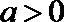
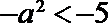
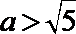
当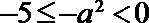
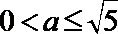
∴
(3)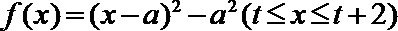
①若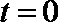
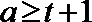
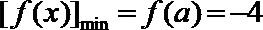
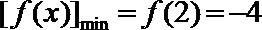
当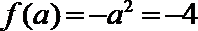
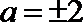
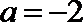
当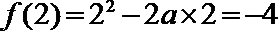
②若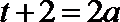
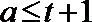
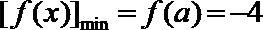
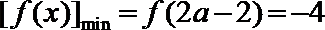
当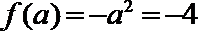
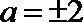
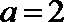
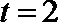
若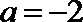
当
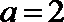
综上所述,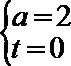
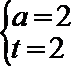
解析
解析已在路上飞奔,马上就到!
知识点
7.函数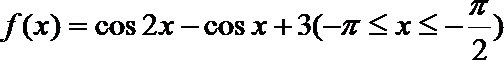
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.对于函数




(1)下面给出两组函数,

第一组:
第二组:
(2)设




(3)设








正确答案
(1)① 设

取


② 设

则


(2)


也即
因为

则
函数



(3)由题意,得



假设存在最大的常数

于是设
=
令

设

设





解析
解析已在路上飞奔,马上就到!
知识点
18.给定函数



(1)若函数




(2)在(1)的条件下,若




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析