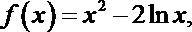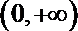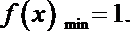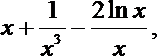- 对数函数的定义
- 共62题
22.已知



(1)当

(2)证明:函数

(3)在(1)的条件下,设函数




正确答案
(1)
(2)证明
(3)
解析
解析已在路上飞奔,马上就到!
知识点
9.已知集合
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,三棱柱







(Ⅰ)求证:

(Ⅱ)求二面角
正确答案
解:
(Ⅰ)依题意,侧面


因为

又平面



平面
所以

(Ⅱ)方法一:由(Ⅰ)知




又



过



则
所以

在

所以
所以
即二面角

方法二:以

由已知可得
故
则
设平面

则

令
显然

所以
即二面角

解析
解析已在路上飞奔,马上就到!
知识点
20.
(1)求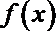
(2)若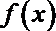
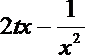
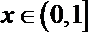
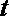
正确答案
解:(1)函数的定义域为
设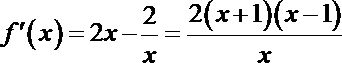

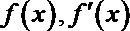
所以,当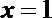
(2)由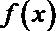
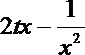
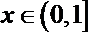
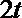
令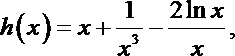
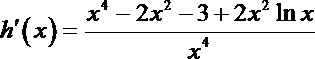
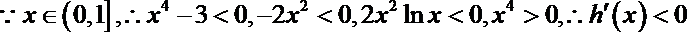
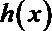
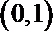
∴当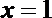
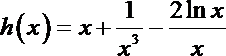
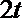
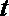
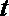
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数
(Ⅰ)若

(Ⅱ)试问:对某个实数



正确答案
解:(Ⅰ)定义域为

则当



当



故函数

(Ⅱ)假设方程

设


则
即

则
设



则当



则


则
故不存在.
解析
解析已在路上飞奔,马上就到!
知识点
12.曲线

正确答案
解析
解



知识点
4. 设

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析