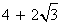- 正弦函数的奇偶性
- 共47题
1
题型:简答题
|
在






正确答案
4
解析
解析:由条件可知
即

由余弦定理


知识点
正弦函数的奇偶性
1
题型:
单选题
|
已知命题



正确答案
D
解析
原命题为特称命题,故其否定为全称命题,即
知识点
正弦函数的奇偶性
1
题型:
单选题
|
已知







正确答案
A
解析
由于



知识点
正弦函数的奇偶性
1
题型:
单选题
|
在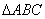
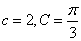
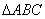
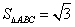
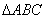
正确答案
A
解析
知识点
正弦函数的奇偶性
1
题型:填空题
|
已知直线的极坐标方程为 
正确答案
解析
知识点
正弦函数的奇偶性
下一知识点 : 正弦函数的定义域和值域
扫码查看完整答案与解析