- 正弦函数的奇偶性
- 共47题
已知函数
(1)求函数
(2)设











正确答案
见解析
解析
(1)
则
最小正周期是
(2)








由余弦定理,得

由①②解得
知识点
已知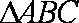
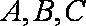
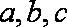
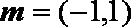
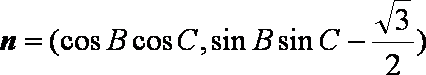

(1)求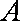
(2)若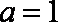
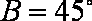
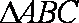
正确答案
见解析。
解析
(1)
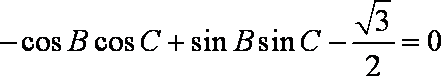
即: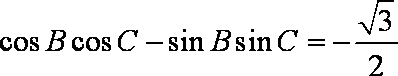

因为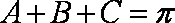
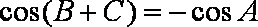
所以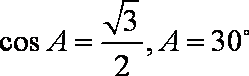
(2)因为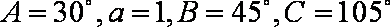
又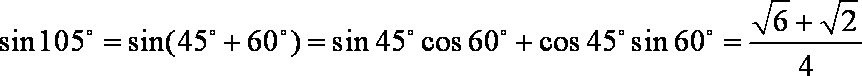
由正弦定理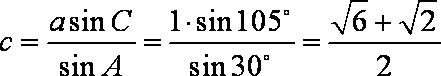
所以
知识点
已知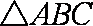
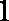
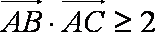
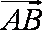
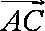
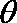
(1)求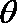
(2)求函数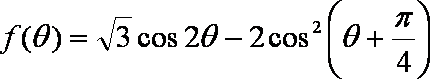
正确答案
见解析。
解析
(1)设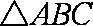
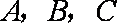
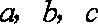
则由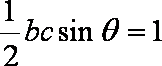
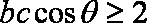
可得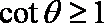
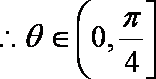
(2)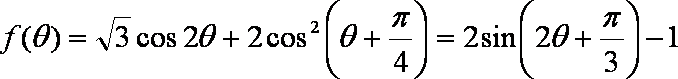
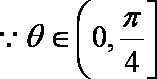
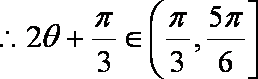
所以,当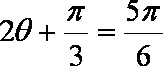
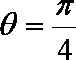

知识点
如图,已知圆







(1)求动点

(2)已知







正确答案
见解析
解析
(1)


得
又



(2)由点











所以
当

知识点
已知椭圆



(1)求椭圆
(2)斜率为





正确答案
见解析
解析
(1)设椭圆


由

∵ 椭圆经过点


∴ 椭圆的方程为
(2)设直线

由
令





知识点
扫码查看完整答案与解析