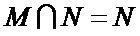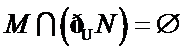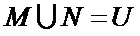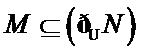- 交、并、补集的混合运算
- 共116题
1．设集合
A
B
C
D
正确答案
解析
因为
考查方向
解题思路
1)解不等式
2)求
易错点
本题易在求集合A的时出现错误，易忽视二元一次不等式中二次项系数应先变为正数，再解不等式；以及只是不等式在解时注意单调性.
知识点
1．已知
A
B
C
D
正确答案
解析
因为
考查方向
解题思路
1）求
易错点
本题易在求集合的交并补运算时出现错误.
知识点
2． 已知全集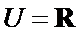
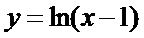
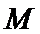
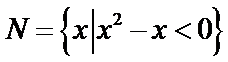
论正确的是
A
B
C
D
正确答案
解析
∵函数 y ＝ln(x－1)的定义域M ＝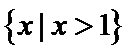
∴
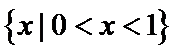
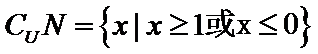
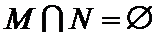
故选 D．
考查方向
解题思路
先化简集合M ＝，N ＝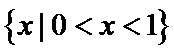
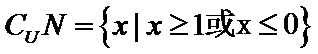
易错点
本题是基础题，解题时只要认真审题，不会出错，属于送分题。
知识点
1.已知集合
正确答案
解析
考查方向
解题思路
1.先分别将集合A,B化简；2.利用数轴求两个集合的交集。
易错点
对于集合A的理解不到位，导致理解成y的范围致错。
知识点
1.已知全集
A
B
C
D
正确答案
解析
结合选项判断，可知C选项为正确选项
考查方向
集合和元素的关系 集合的运算
解题思路
根据集合和元素的关系，集合的运算性质求解
易错点
考虑问题不全面，马虎大意
教师点评
简单题，对集合的相关性质的考察
知识点
9．设集合A={x∈N| 
正确答案
解析
由x∈N，
由B中y=ln（x-1），得到x-1＞0，即x＞1，
∴B={x|x＞1}，∁RB={x|x≤1}，
则A∩（∁RB）={0，1}，
故答案为：{0，1，2，5}；{x|x＞1}；{0，1}
考查方向
对数函数的定义域
交、并、补集的混合运算
解题思路
根据x∈N，
易错点
不能熟练掌握集合的定义和集合间的关系
知识点
扫码查看完整答案与解析