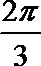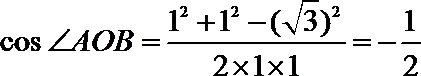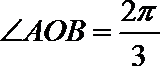与球体有关的内切、外接问题
共52题

· 与球体有关的内切、外接问题

与球体有关的内切、外接问题
共52题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

10．如图，正方体的棱长为，以顶点A为球心，2为半径作一个球，则图中球面与正方体的表面相交所得到的两段弧长之和等于（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

球面距离及相关计算与球体有关的内切、外接问题

题型：单选题

单选题 · 5 分

10.已知正四棱锥的底面边长为，高为，球是正四棱锥的内切球，则球的表面积为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

球的体积和表面积与球体有关的内切、外接问题

题型：单选题

单选题 · 5 分

6．已知球的表面积为20，球面上有A、B、C三点，如果AB=AC=2，BC=2，则球心到平面ABC的距离为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

与球体有关的内切、外接问题

题型：填空题

填空题 · 5 分

14．如图，已知长方体的各顶点都在同一球面上，且,则这个球的体积为（）．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

球的体积和表面积与球体有关的内切、外接问题

题型：单选题

单选题 · 5 分

10．已知正方形的边长为4，点位边的中点，沿折叠成一个三棱锥（使重合于点），则三棱锥的外接球表面积为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

球的体积和表面积与球体有关的内切、外接问题

题型：单选题

单选题 · 5 分

11．已知正方形的边长为4，点位边的中点，沿折叠成一个三棱锥（使重合于点），则三棱锥的外接球表面积为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

球的体积和表面积与球体有关的内切、外接问题

题型：填空题

填空题 · 5 分

16．表面积为的球面上有四点S、A、B、C，且是等边三角形，球心O到平面ABC的距离为，若平面平面,则棱锥体积的最大值为___________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

棱柱、棱锥、棱台的体积与球体有关的内切、外接问题平面与平面垂直的判定与性质

题型：填空题

填空题 · 5 分

9.如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,以该多面体的各条棱中最长的棱为标准截取8根等长的铁丝接成如图的四棱锥形骨架,把一个皮球放入该四棱锥形骨架内,使皮球的表面与8根铁丝都相切,则皮球的表面积为________.

正确答案

36π

解析

如图所示,原几何体为三棱锥D-ABC,

其中AB=BC=4,AC=4,DB=DC=2,DA==6,

故最长的棱的长度为DA=6.

又因为四棱锥形骨架的底面是一个正方形,一共有四条棱,又正方形的中心到四条棱的距离为3,所以皮球的表面与8根铁丝都相切时,球心为底面正方形的中心,所以球的半径是3 cm,所以球的表面积为36π.

知识点

简单空间图形的三视图球的体积和表面积与球体有关的内切、外接问题

题型：单选题

单选题 · 5 分

6.在边长为1的正方形ABCD内任取一点P,则动点P到点A和C的距离都小于1的概率是（　　）.

A1-

B-1

D2-

正确答案

解析

满足条件的正方形ABCD如图所示,

其中满足条件的动点P的平面区域如图中阴影部分,

则正方形的面积S正方形=1,

阴影部分的面积S阴影=×2-1=-1.

故所求事件的概率为

知识点

棱柱、棱锥、棱台的体积球的体积和表面积与球体有关的内切、外接问题与面积、体积有关的几何概型

题型：填空题

填空题 · 4 分

10．已知四面体的外接球球心在棱上，，，则、两点在四面体的外接球上的球面距离是___________．

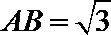
正确答案

解析

由四面体的外接球球心在棱上，，得

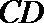
球的半径

∴

∴、两点在四面体的外接球上的球面距离为．

考查方向

本题考查球面距离及其相关计算，考查空间想象能力、计算、逻辑思维能力，是中档题．

解题思路

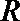
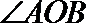
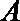
先求球半径，再求的大小，然后利用公式求得、两点在四面体的外接球上的球面距离．

易错点

在球上的位置关系不明确，从而影响球面距离的求解．

知识点

球面距离及相关计算与球体有关的内切、外接问题

继续学习棒棒哒，已是最后一个知识点

已完结

百度题库 > 高考 > 理科数学 > 与球体有关的内切、外接问题

扫码查看完整答案与解析