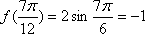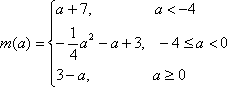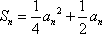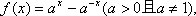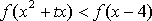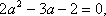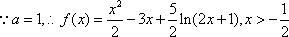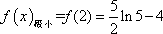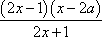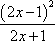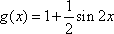- 函数的概念与基本初等函数
- 共8430题
已知函数
(1)求函数
(2)求函数

正确答案
(1)
解析
解析:(1)
所以函数

(2)
∵



∴
另解:
∵


∴

知识点
已知函数

(1)判断函数
(2)求



正确答案
见解析
解析
解析:(1)f(x)的定义域为
f(-x)=log2

所以,f(x)为奇函数. ………………………………………..6分
(2)由y=

所以,f -1(x)= 

因为函数
所以,

所以,log2k=

从而,k
知识点
已知函数

(1)求
(2)若 

正确答案
见解析。
解析
(1)








则 
(2)由已知得

则

知识点
已知函数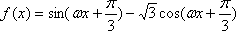
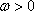
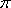
(1)求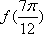
(2)若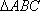
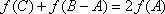
正确答案
见解析。
解析
(1)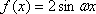
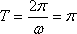
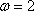
(2)由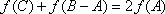
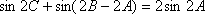
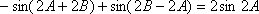
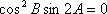
所以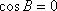
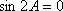
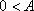
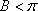
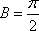
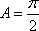
知识点
已知函数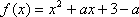
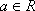
(1)求
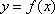
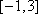
(2)当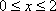
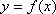

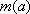
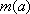

(3)对于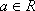
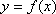
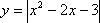
正确答案
见解析
解析
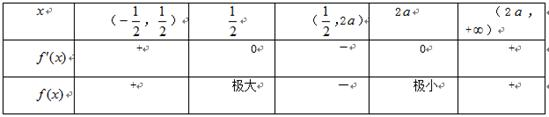
(1)函数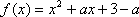
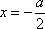
因为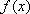
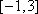
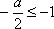
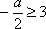
故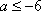
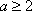
(2)当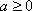
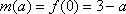
当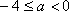
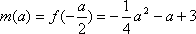
当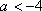
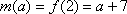
所以,
分段讨论并比较大小得,当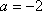
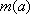
(3)公共点的横坐标
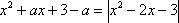

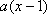
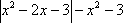
设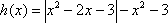
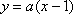
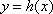
当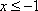
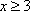
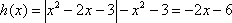
解方程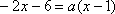
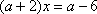
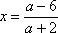
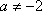
当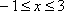
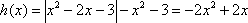
解方程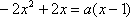
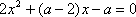
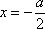
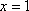
研究结论及评分示例:(满分6分)
结论1:无论
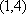
结论2:(对某些具体的
当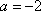
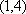
当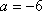
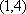
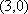
当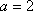
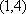
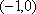
(对每一个具体的
结论3:当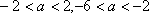
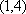
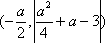
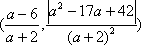
结论4:叙述完整,结论正确,给满分.具体包括下面几个方面:
当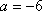
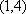
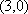
当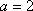
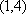
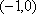
当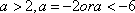
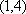
当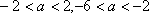
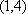
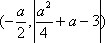
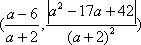
知识点
已知函数
(1)求函数


(2)如果当




(3)对任意的



正确答案
见解析
解析
解析:(1)令


对任意
所以函数
另证:对任意
所以函数
(2)由


因为


又因为


且


故






所以

(3)假设存在
即

解得

下证:
证明:

∴

所以存在

另证:要证明





∴
所以存在
知识点
定义:对函数





(1) 判断函数

(2) 若函数

(3) 已知函数


正确答案
见解析
解析
(1)若存在


……………………………. 2分



“k性质函数”。 ……………………………. 4分
(2)由

即


当

当




综上,
……………………………. 10分
(3)由条件存在




……………………………. 12分

令
则


……………………………. 16分
知识点
已知函数


(1)求实数
(2)已知结论:若函数








正确答案
见解析
解析
解:(1)



当



当







(2)令
则





使得












故对任意
知识点
设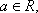
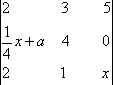
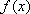

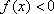
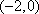
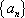

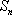
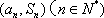
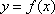
(1)求函数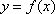
(2)若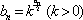
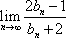
(3)令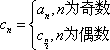
正确答案
见解析
解析
(1)由条件可知,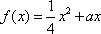
因为关于
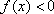
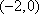
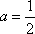
即函数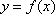
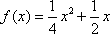
(2)因为点列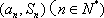
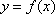
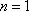
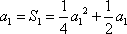
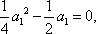
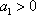
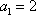
当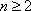
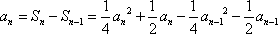
化简得: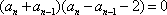
因为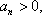
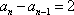
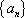
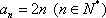
则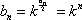
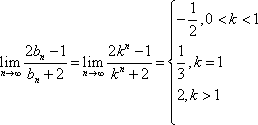
(3)在数列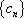

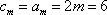
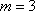

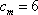
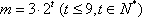
所以,满足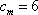
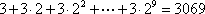
知识点
已知函数
(1)求函数
(2)在△





正确答案
见解析。
解析
(1)
∵
∴
∴函数
(2)
∴


在


∴
解得
∵

知识点
设函数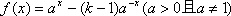
(1)求k值;
(2)若f(1)<0,试判断函数单调性并求使不等式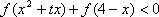

(3)若f(1)=,且g(x)=a 2x+a - 2x-2m f(x) 在[1,+∞)上的最小值为-2,求m的值。
正确答案
见解析
解析
(1)∵f(x)是定义域为R的奇函数,
∴f(0)=0, …………………… 2分
∴1-(k-1)=0,∴k=2, …………………… 4分
(2)
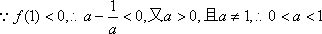
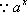
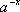
不等式化为
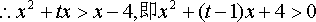
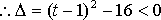
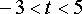
(3)∵f(1)=,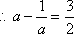
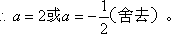
∴g(x)=22x+2-2x-2m(2x-2-x)=(2x-2-x)2-2m(2x-2-x)+2.
令t=f(x)=2x-2-x,
由(1)可知f(x)=2x-2-x为增函数
∵x≥1,∴t≥f(1)=,
令h(t)=t2-2mt+2=(t-m)2+2-m2 (t≥)………………15分
若m≥,当t=m时,h(t)min=2-m2=-2,∴m=2………… 16分
若m<,当t=时,h(t)min=-3m=-2,解得m=>,舍去
……………………17分
综上可知m=2. ………………………………18分
知识点
已知函数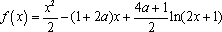
(1)设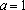
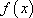
(2)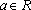
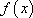
正确答案
见解析。
解析
(1)
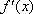

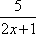
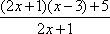
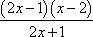
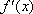



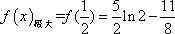
(2)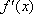


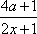
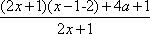
令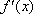



i、当2



所以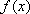






ii、当2



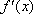



所以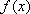
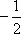

iii、当





所以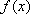






iv、当2

所以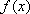




综上述:
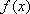







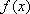








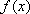
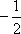



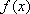






知识点
已知函数
(1)求
(2)当

正确答案
见解析。
解析

(1)函数

由正弦函数的性质知,当
即




(2)因为


所以

知识点
已知函数

(1)若

(2)若

(3)设





正确答案
见解析。
解析
(1)当

则
当



则函数

(2)


设












(3)

因为对任意的


所以
即
即

设





所以

知识点
已知函数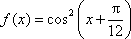
(1)设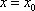
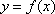
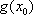
(2)求函数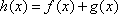
正确答案
见解析。
解析
(1)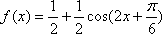
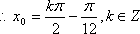
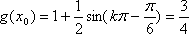

(2)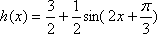
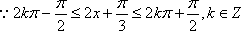
增区间为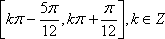
知识点
扫码查看完整答案与解析