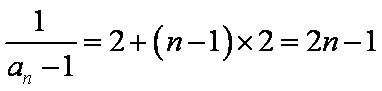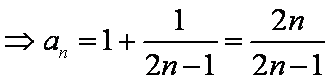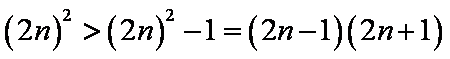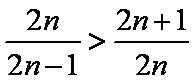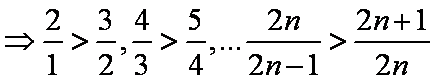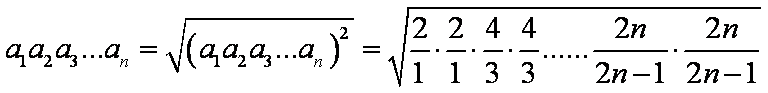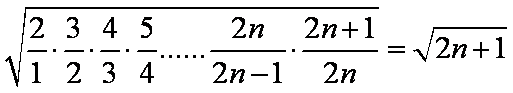- 导数及其应用
- 共3028题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
已知函数
(1)若a=2,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)求f(x)在区间[2,3]上的最大值和最小值。
正确答案
见解析
解析
(1)解:f(x)的定义域为R,且 f'(x)=2x2﹣4x+2﹣a,当a=2时,
所以曲线y=f(x)在点(1,f(1))处的切线方程为 
(2)解:方程f'(x)=0的判别式为△=(﹣4)2﹣4×2×(2﹣a)=8a。
1)当a≤0时,f'(x)≥0,所以f(x)在区间(2,3)上单调递增,所以f(x)在区间[2,3]
上的最小值是
2)当a>0时,令f'(x)=0,得 

故f(x)的单调增区间为


①当0<a≤2时,x2≤2,此时f(x)在区间(2,3)上单调递增,所以f(x)在区间[2,3]
上的最小值是
②当2<a<8时,x1<2<x2<3,此时f(x)在区间(2,x2)上单调递减,在区间(x2,3)上单调递增,
所以f(x)在区间[2,3]上的最小值是 
因为 
所以 当


③当a≥8时,x1<2<3≤x2,此时f(x)在区间(2,3)上单调递减,
所以f(x)在区间[2,3]上的最小值是f(3)=7﹣3a;最大值是
综上可得,
当a≤2时,f(x)在区间[2,3]上的最小值是
当

当


当a≥8时,f(x)在区间[2,3]上的最小值是7﹣3a,最大值是
知识点
在







(1)若


(2)设

正确答案
(1)4
(2)
解析
(1)因为
所以
因为
所以
因为


所以
所以

(2)因为
所以

因为
所以
所以当



知识点
已知函数
(1)求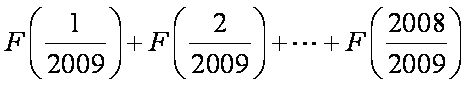
(2)已知数列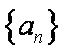
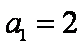
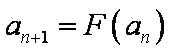
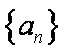
(3) 求证: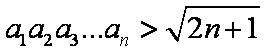
正确答案
见解析
解析
解析:(1)因为
所以设S=
S=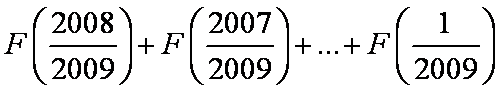
(1)+(2)得:
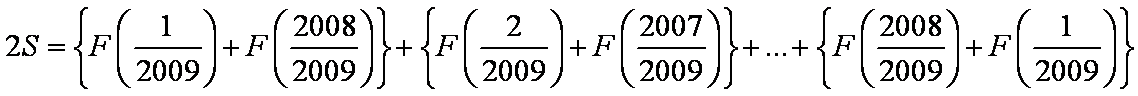
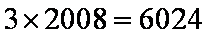
(2)由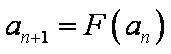
所以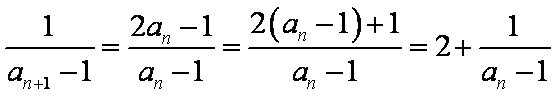
所以
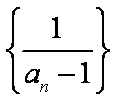

所以
(3)因为
所以
所以
>
知识点
设

(1)当

(2)若


正确答案
(1)

解析
对

(1)当


结合①,可知
所以,

(2)若

在R上恒成立,因此

知识点
函数
正确答案
解析
略
知识点
已知点


①
②当

③
④当




其中,所有正确说法的序号是 .
正确答案
③④
解析
略
知识点
给一个正方体的六个面涂上四种不同颜色(红、黄、绿、兰),要求相邻两个面涂不同的颜色,则共有涂色方法(涂色后,任意翻转正方体,能使正方体各面颜色一致,我们认为是同一种涂色方法( )
正确答案
解析
解:由于涂色过程中,要保证满足用四种颜色,且相邻的面不同色,对于正方体的三对面来说,必然有两对同色,一对不同色,而且三对面具有“地位对等性”,因此,只需从四种颜色中选择2种涂在其中两对面上,剩下的两种颜色涂在另外两个面即可,因此共有
故选A。
知识点
设



正确答案
解析
画出可行域,可知



知识点
设函数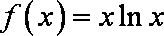
(1)求函数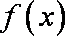
(2)设
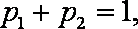
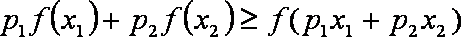
(3)设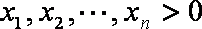
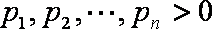
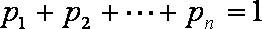
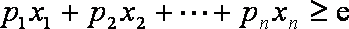
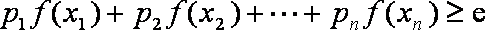
正确答案
见解析
解析
(1)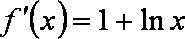
由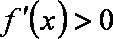
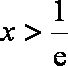
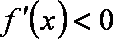
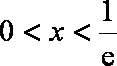
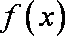
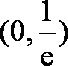
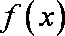
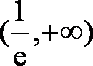
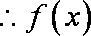
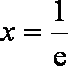
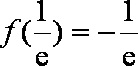
(2)令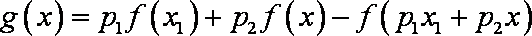
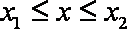
则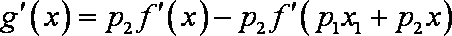
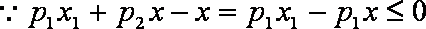
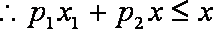
而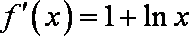
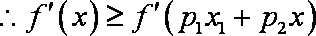
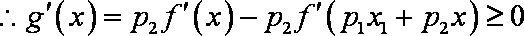
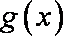
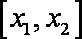
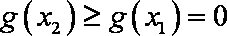
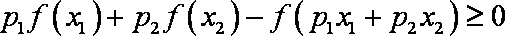
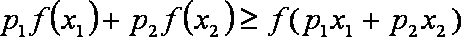
(3)先证明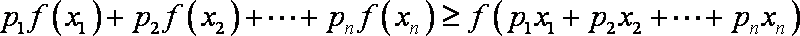
当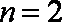
假设当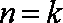
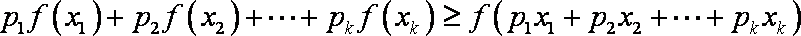
当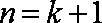
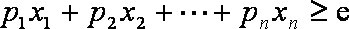
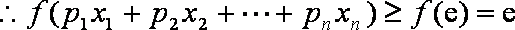
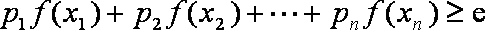
知识点
某地区对12岁儿童瞬时记忆能力进行调查,瞬时记忆能力包括听觉记忆能力与视觉记忆能力.某班学生共有40人,下表为该班学生瞬时记忆能力的调查结果,例如表中听觉记忆能力为中等,且视觉记忆能力偏高的学生为3人。
由于部分数据丢失,只知道从这40位学生中随机抽取一个,视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上的概率为
(1)试确定

(2)从40人中任意抽取3人,求其中至少有一位具有听觉记忆能力或视觉记忆能力超常的学生的概率;
(3)从40人中任意抽取3人,设具有听觉记忆能力或视觉记忆能力偏高或超常的学生人数为


正确答案
(1)a=6,b=2(2)
解析
(1)由表格数据可知,视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上的学生共有

则

所以
答:

(2)由表格数据可知,具有听觉记忆能力或视觉记忆能力超常的学生共有8人。
方法1:记“至少有一位具有听觉记忆能力或视觉记忆能力超常的学生”为事件
则“没有一位具有听觉记忆能力或视觉记忆能力超常的学生”为事件
所以
答:从这40人中任意抽取3人,其中至少有一位具有听觉记忆能力或视觉记忆能力超常的学生的概率为
方法2:记“至少有一位具有听觉记忆能力或视觉记忆能力超常的学生”为事件
所以
答:从这40人中任意抽取3人,其中至少有一位具有听觉记忆能力或视觉记忆能力超常的学生的概率为
(3)由于从40位学生中任意抽取3位的结果数为


所以从40位学生中任意抽取3位,其中恰有



因为



所以
所以
答:随机变量

知识点
如图,在边长为π的正方形内的正弦曲线
正确答案
解析
区域M的面积为:SM=



知识点
设函数
(1) 判断

(2) 若不等式




(3)设





正确答案
见解析
解析
解析:(1)∵ 

设


∴




∴


(2)①∵











②显然当

当


下面证明一个更强的不等式:

即



由(1) 知



∴不等式②成立,从而①成立 又
∴
综合上面∴





知识点
已知数列
(1)求
(2)已知存在实数



(3)记




正确答案
见解析
解析
解析:(1)




(2)
=
=




由题意,令

(3)由(2)知
所以
此时
=

>
知识点
已知不等式



正确答案
见解析。
解析
因为

又


解得
知识点
扫码查看完整答案与解析