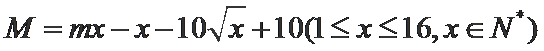- 函数的概念与基本初等函数
- 共8430题
14.设函数
①若a=0,则f(x)的最大值为____________________;
②若f(x)无最大值,则实数a的取值范围是_________________。
正确答案
2,a<-1
知识点
17. 某油库的设计容量为30万吨,年初储量为10万吨,从年初起计划每月购进石油 




(1)试写出第


(2)要使16个月内每月按计划购进石油之后,油库总能满足区域内和区域外的需求,且每月石油调出后,油库的石油剩余量不超过油库的容量,试确定
正确答案
见解析
解析
解:(1)
(2)根据题意
所以
即 
考查方向
解题思路
本题考查函数不等式的应用.解题步骤如下:
(1)求出函数表达式。
(2)根据函数值域,列出不等式。
(3)用换元法求出
易错点
不等式恒成立分析不够
知识点
10.已知函数


正确答案
解析
函数f(x)的定义域为:
关于原点对称,因为x>0时,-x<0,f(-x)=-lnx+x=f(x)
同理可知,当x<0时,f(-x)=f(x),所以f(x)为偶函数
所以f(x)在
所以当m>0时,由



所以此题选B
考查方向
分段函数的性质,偶函数的性质,函数的单调性
解题思路
先求出定义域,然后判断函数的单调性和奇偶性
然后根据奇偶性的性质,求出参数的取值范围
易错点
讨论函数性质时错误,判断函数奇偶性错误
教师点评
分段函数多涉及到分类讨论,学生在解题时要充分注意到
知识点
15.某商品一直打7折出售,利润率为

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.因发生意外交通事故,一辆货车上的某种液体泄露到一鱼塘中。为治理污染,根据环保部门的建议,现决定在鱼塘中投放一种可与污染液体发生化学反应的药剂。已知每投放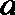
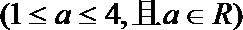
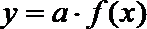
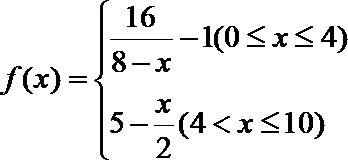
(1)若一次投放4个单位的药剂,则有效治污的时间可达几天?
(2)若因材料紧张,第一次只能投放2个单位的药剂,6天后再投放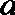
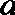
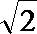
正确答案
(1)因为 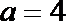
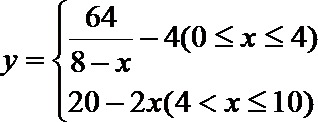
①当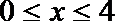
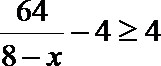
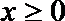
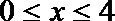
②当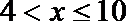
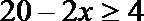
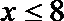
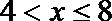
综合得,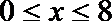
(2) 当
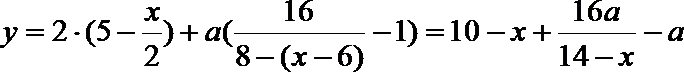
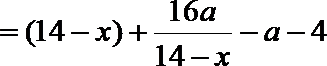
由题意知,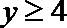
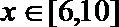
因为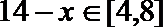
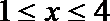
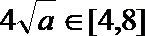
故当且仅当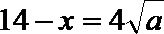
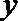

令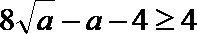
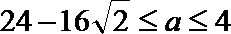
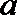
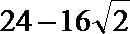
又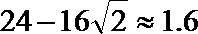
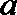
解析
解析已在路上飞奔,马上就到!
知识点
17.为了研究某种药物,用小白鼠进行试验,发现药物在血液内的浓度与时间的关系因使用方式的不同而不同。若使用注射方式给药,则在注射后的3小时内,药物在白鼠血液内的浓度




(1)若a=1,求3小时内,该小白鼠何时血液中药物的浓度最高,并求出最大值?
(2)若使小白鼠在用药后3小时内血液中的药物浓度不低于4,求正数a的取值范围。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 某油库的设计容量为30万吨,年初储量为10万吨,从年初起计划每月购进石油 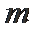
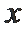
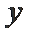
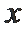

(1)试写出第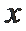
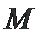
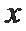
(2)要使16个月内每月按计划购进石油之后,油库总能满足区域内和区域外的需求,且每月石油调出后,油库的石油剩余量不超过油库的容量,试确定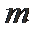
正确答案
见解析
解析
解:(1)
(2)根据题意
所以
即 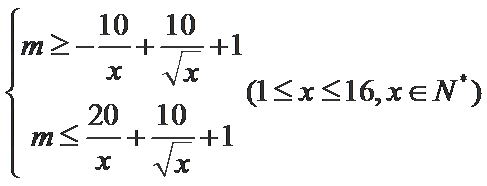
考查方向
解题思路
本题考查函数不等式的应用.解题步骤如下:
(1)求出函数表达式。
(2)根据函数值域,列出不等式。
(3)用换元法求出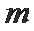
易错点
不等式恒成立分析不够
知识点
如图,某人在垂直于水平地面ABC的墙面前的点A处进行射击训练.已知点A到墙面的距离为AB,某目标点P沿墙面上的射击线CM移动,此人为了准确瞄准目标点P,需计算由点A观察点P的仰角





正确答案
解析
∵AB=15cm,AC=25cm,∠ABC=90°,∴BC=20cm,
过P作PP′⊥BC,交BC于P′,
1当P在线段BC上时,连接AP′,则
设BP′=x,则CP′=20-x,(
由∠BCM=30°,得
在直角△ABP′中,
∴
令
∴x=0时,
2当P在线段CB的延长线上时,连接AP′,则
设BP′=x,则CP′=20+x,(
由∠BCM=30°,得
在直角△ABP′中,
∴
令

所以,当


所以当
此时

综合1,2可知
知识点
设







正确答案
解析
略
知识点
20.小明同学制作了一个简易的网球发射器,可用于帮忙练习定点接发球,如图1所示,网球场前半区、后半区总长为23.77米,球网的中间部分高度为0.914米,发射器固定安










正确答案
(1)由




(Ⅱ)网球发过球网,满足
所以

因此

依题意:关于k的方程 

即

得

解析
本题是函数的应用,将实际问题与函数联系起来,有利于学生对函数的理解。
考查方向
函数的应用
解题思路
最大射程就是最大值,是网球落地的横坐标
易错点
实际问题和函数模型的转换
知识点
13.某食品的保鲜时间y(单位:小时)与储存温度x(单位:





正确答案
24
考查方向
易错点
1.没有发现192与48之间的关系导致不会解方程组;
知识点
建设项目的保修证书的主要内容包括( )。
A.保修时间
B.保修说明
C.保修单位的名称
D.保修所使用的材料
E.保修范围和内容
正确答案
A,B,C,E
解析
暂无解析
某山区外围有两条相互垂直的直线型公路,为进一步改善山区的交通现状,计划修建一条连接两条公路和山区边界的直线型公路,记两条相互垂直的公路为l1,l2,山区边界曲线为C,计划修建的公路为l,如图所示,M,N为C的两个端点,测得点M到l1,l2的距离分别为5千米和40千米,点N到l1,l2的距离分别为20千米和2.5千米,以l2,l1在的直线分别为x,y轴,建立平面直角坐标系xOy,假设曲线C符合函数y=
21.求a,b的值;
22.设公路l与曲线C相切于P点,P的横坐标为t.
①请写出公路l长度的函数解析式f(t),并写出其定义域;
②当t为何值时,公路l的长度最短?求出最短长度.
正确答案
解析
(1)由题意知,点M,N的坐标分别为(5,40),(20,2.5),
将其分别代入y=

解得
考查方向
解题思路
由题意知,点M,N的坐标分别为(5,40),(20,2.5),将其分别代入y=
易错点
本题考查利用数学知识解决实际问题,在实际应用问题时易错.
正确答案
t=10

解析
)①由(1)y=

∴y′=﹣
∴切线l的方程为y﹣

设在点P处的切线l交x,y轴分别于A,B点,则A(

∴f(t)=

②设g(t)=


t∈(5,10

从而t=10
∴g(t)min=300,
∴f(t)min=15
答:t=10

考查方向
解题思路
①求出切线l的方程,可得A,B的坐标,即可写出公路l长度的函数解析式f(t),并写出其定义域;
②设g(t)=
易错点
本题考查利用数学知识解键决实际问题,考查导数知识的综合运用,确定函数关系,在应用导数解题过程中易错.
已知
正确答案
解析



知识点
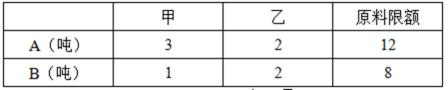
8.某企业生产甲乙两种产品均需用A,B两种原料,已知生产1吨每种产品需原料及每天原料的可用限额如表所示,如果生产1吨甲、乙产品
正确答案
解析
设每天生产甲乙两种产品分别为x,y顿,利润为z元,
则3x+2y≤12x+2y≤8x≥0,y≥0, 目标函数为 z=3x+4y.
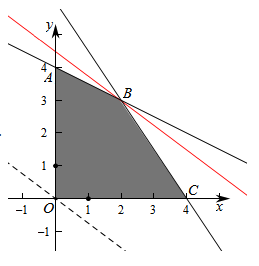
作出二元一次不等式组所表示的平面区域(阴影部分)即可行域。
由z=3, 即B的坐标为x=2,y=3,
∴Zmax=3x+4y=6+12=18.
即每天生产甲乙两种产品分别为2,3顿,能够产生最大的利润,最大的利润是18万元,
考查方向
本题主要考查应用题、线性规划最优解等知识,意在考查考生的理解问题解决问题的能力和数形结合的能力.
解题思路
设每天生产甲乙两=3x+4y得y=-34x+z4,
平移直线y=-34x+z4由图象可知当直线y=-34x+z4经过点B时,直线y=-34x+z4的截距最大, 此时z最大,
解方程组3x+2y=12x+2y=8,解得x=2y=分别为x,y顿,利润为z元,然后根据题目条件建立约束条件,得到目标函数,画出约束条件所表示的区域,然后利用平移法求出z的最大值.
易错点
1.不会根据题意设变量表示题中的约束条件;
2.不会利用线性规划求目标函数的最值。
教师点评
考生需要掌握目标函数的设立,了解约束条件并作图标,利用线性规划求目标函数的最值。
知识点
扫码查看完整答案与解析