- 平行向量与共线向量
- 共100题
如图,在平面直角坐标系xOy中,M,N分别是椭圆

(1)若直线PA平分线段MN,求k的值;
(2)当k=2时,求点P到直线AB的距离d;
(3)对任意的k>0,求证:PA⊥PB.
正确答案
见解析
解析
(1)由题设知,a=2,b=




(2)直线PA的方程为y=2x,代入椭圆方程得




于是C


因此,
(3)解法一:将直线PA的方程y=kx代入



故直线AB的斜率为

解得

于是直线PB的斜率
因此k1k=-1,所以PA⊥PB.
解法二:设P(x1,y1),B(x2,y2),则x1>0,x2>0,x1≠x2,A(-x1,-y1),C(x1,0).设直线PB,AB的斜率分别为k1,k2.因为C在直线AB上,所以
因此k1k=-1,所以PA⊥PB.
知识点
若集合

正确答案
解析

知识点
已知f(x)=m(x-2m)(x+m+3),g(x)=
①
②
则m的取值范围是
正确答案
解析
根据


































知识点
设集合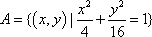
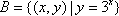
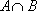
正确答案
解析
画出椭圆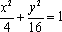
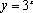

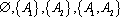
知识点
设变量x,y满足约束条件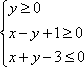
正确答案
解析
略
知识点
扫码查看完整答案与解析