- 平行向量与共线向量
- 共100题
1
题型:
单选题
|
2.已知O、A、M、B为平面上四点,且
正确答案
B
解析
解析已在路上飞奔,马上就到!
知识点
平行向量与共线向量平面向量的基本定理及其意义
1
题型:简答题
|
20.若a,b是两个不共线的非零向量,t∈R.
(1)若a,b起点相同,t为何值时,a,tb,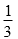
(2)若|a|=|b|,且a与b夹角为60°,t为何值时,|a-tb|的值最小?
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
向量的模平行向量与共线向量两向量的和或差的模的最值数量积表示两个向量的夹角
1
题型:填空题
|
11. 已知向量
正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
平行向量与共线向量平面向量的坐标运算
1
题型:简答题
|
18.已知△ABC的角A、B、C所对的边分别是a、b、c,
设向量
(1)若
(2)若




正确答案
证明:(1)∵m∥n
∴asinA=bsinB
即a•

∴a=b ∴△ABC为等腰三角形.
(2)由题意,m•p=0
∴a(b﹣2)+b(a﹣2)=0
∴a+b=ab
由余弦定理4=a2+b2﹣2ab•cos
∴4=a2+b2﹣ab=(a+b)2﹣3ab
∴ab2﹣3ab﹣4=0
∴ab=4或ab=﹣1(舍去)
∴S△ABC=
=

解析
解析已在路上飞奔,马上就到!
知识点
平行向量与共线向量
1
题型:填空题
|
14.关于平面向量a,b,c,有下列三个命题:
①若a·b=a·c,则b=c.
②若a=(1,k),b=(-2,6),a∥b,则k=-3.
③非零向量a和b满足|a|=|b|=|a-b|,则a与a+b的夹角为60°.
其中真命题的序号为______.(写出所有真命题的序号)
正确答案
②
解析
解析已在路上飞奔,马上就到!
知识点
向量的模平行向量与共线向量相等向量与相反向量平面向量数量积的运算数量积表示两个向量的夹角
下一知识点 : 相等向量与相反向量
扫码查看完整答案与解析


