- 平行向量与共线向量
- 共100题
10.在平面内,定点A,B,C,D满足












正确答案
解析
由题意,






同理可得,






所以正三角形

我们以



由



而


可以写出
则
当


考查方向
解题思路
本题考查平面向量的数量积与向量的模,由于结论是要求向量模的平方的最大值,因此我们要把它用一个参数表示出来,解题时首先对条件进行化简变形,本题中得出




易错点
本题考查平面向量的数量积与向量的模,在求向量模的平方的最大值易错
知识点
14.函数

正确答案
知识点
3.已知向量


正确答案
解析
试题分析:向量



考查方向
解题思路
直接根据向量的坐标运算公式及向量垂直的坐标表示进行计算。
易错点
不熟悉向量的坐标运算公式导致出错。
知识点
13.设向量a,b不平行,向量λa+b与a+2b平行,则实数λ=________.(用数字填写答案)
正确答案
知识点
7.从1894年中状元,到1926年在破产风波中凄然弃世,张謇这三十
正确答案
解析
本题考查的是民族工业发展的相关知识内容。中国近代的民族工业在帝国主义、封建主义和官僚资本主义三座大山的夹缝中求生存、图发展。艰难曲折的根源在于半殖民地半封建的社会性质。A项、B项、D项都不是其艰难的根源。故正确答案选择C项。
考查方向
解题思路
本题考查的是民族工业发展的相关知识内容。中国近代的民族工业在帝国主义、封建主义和官僚资本主义三座大山的夹缝中求生存、图发展。艰难曲折的根源在于半殖民地半封建的社会性质。
易错点
此题易错点在于不能够把握民族工业艰难发展的根源所在而误选
知识点
已知a,b,c分别为△ABC内角A,B,C的对边,sin2B=2sinAsinC
17.若a=b,求cosB;
18.设B=90°,且a=
正确答案
正确答案
在△ABC中,角A,B,C的对边分别为a,b,c,向量

16.求角
17.若a=6,求△ABC面积的最大值.
正确答案
(Ⅰ)
解析
试题分析:本题属于三角函数的基本问题,题目的难度是逐渐由易到难,(1)直接按步骤来求解,(2)要注意注明基本不等式等号成立的条件.
(Ⅰ)因为向量

所以
由正弦定理得
即
由于B是三角形的内角,
则

考查方向
解题思路
本题考查平面向量共线的坐标表示、解三角形,解题步骤如下:
1)利用平面向量共线的坐标表示得到三角形的边角关系;
2)利用正弦定理将边角关系转化为角角关系,利用三角形的内角和定理进行求解;
3)利用余弦定理得到边边关系;
4)利用基本不等式和三角形的面积公式进行求解。
易错点
1)易混淆平面向量共线的坐标表示与垂直的坐标表示;
2)利用基本不等式求最值时,忽视注明等号成立的条件.
正确答案
(Ⅱ)
解析
试题分析:本题属于三角函数的基本问题,题目的难度是逐渐由易到难,(1)直接按步骤来求解,(2)要注意注明基本不等式等号成立的条件.
(Ⅱ)因为
所以
且仅当b=c时取得等号,所以
故
所以当b=c时,

考查方向
解题思路
本题考查平面向量共线的坐标表示、解三角形,解题步骤如下:
1)利用平面向量共线的坐标表示得到三角形的边角关系;
2)利用正弦定理将边角关系转化为角角关系,利用三角形的内角和定理进行求解;
3)利用余弦定理得到边边关系;
4)利用基本不等式和三角形的面积公式进行求解。
易错点
1)易混淆平面向量共线的坐标表示与垂直的坐标表示;
2)利用基本不等式求最值时,忽视注明等号成立的条件.
已知平面向量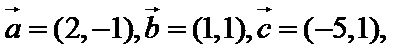
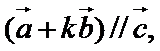
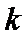
正确答案
解析
由

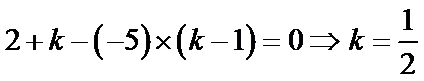
考查方向
解题思路
由
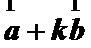
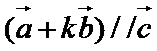

易错点
本题易在坐标运算上出错。
知识点
2.已知向量a=(2,x).b=(一4,2).若(a十b)∥(2a-b),则实数x的值为( )
正确答案
解析
试题分析:本题属于平面向量中的基本问题,题目的难度是简单。
考查方向
本题主要考查了平面向量的平行的坐标表示,在近几年的各省高考题出现的频率较高。
解题思路
本题考查平面向量的位置关系,解题步骤如下:
(1)由题可知,易得a+b=(-2,x+2),2a-b=(8,2x-2)。
(2)令8(x+2)=-2(2x-2),解得x= -1.
易错点
本题易在应用平行的坐标表示公式时发生错误。
知识点
17.已知数列{an}的前n项和为Sn ,向量a= (S n ,1),b= (2n — 1, 


①求数列{bn}的通项公式,
②设Cn =
正确答案
(1)
(2)①
解析
(1)∵






(2)①∵








考查方向
数列的通项公式和求和
解题思路
(1)利用
(2)①利用

易错点
1、利用定义求通项公式
2、第二问中错位相减法计算的准确性;
知识点
扫码查看完整答案与解析