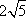- 直线方程和两条直线的位置关系
- 共550题
直线x+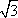
正确答案
解析
圆心O到直线AB的距离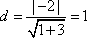
所以
知识点
若变量x,y满足约束条件
正确答案
6
解析
知识点
已知平面α截一球面得圆






正确答案
解析
如图所示,由圆











知识点
如图所示,程序框图(算法流程图)的输出结果是 .
正确答案
15
解析
略
知识点
已知数列{an}的前n项和Sn=kcn-k(其中c,k为常数),且a2=4,a6=8a3.
(1)求an;
(2)求数列{nan}的前n项和Tn.
正确答案
(1) an=2n. ;(2) (n-1)2n+1+2.
解析
(1)由Sn=kcn-k,
得an=Sn-Sn-1=kcn-kcn-1(n≥2),
由a2=4,a6=8a3,得kc(c-1)=4,kc5(c-1)=8kc2(c-1),
解得
于是an=2n.
(2)
Tn=2+2·22+3·23+4·24+…+n·2n,
Tn=2Tn-Tn=-2-22-23-24-…-2n+n·2n+1=-2n+1+2+n·2n+1=(n-1)2n+1+2.
知识点
已知函数f(x)=ax3+bx+c在点x=2处取得极值c-16.
(1)求a,b的值;
(2)若f(x)有极大值28,求f(x)在[-3,3]上的最小值。
正确答案
(1) a=1,b=-12. ;(2) -4
解析
(1)因f(x)=ax3+bx+c,故f′(x)=3ax2+b,
由于f(x)在点x=2处取得极值c-16,
故有
即
解得a=1,b=-12.
(2)由(1)知f(x)=x3-12x+c;
f′(x)=3x2-12=3(x-2)(x+2)。
令f′(x)=0,得x1=-2,x2=2.
当x∈(-∞,-2)时,f′(x)>0,故f(x)在(-∞,-2)上为增函数;
当x∈(-2,2)时,f′(x)<0,故f(x)在(-2,2)上为减函数;
当x∈(2,+∞)时,f′(x)>0,故f(x)在(2,+∞)上为增函数。
由此可知f(x)在x1=-2处取得极大值f(-2)=16+c,f(x)在x2=2处取得极小值f(2)=c-16.
由题设条件知16+c=28得c=12.
此时f(-3)=9+c=21,f(3)=-9+c=3,f(2)=-16+c=-4,
因此f(x)在[-3,3]上的最小值为f(2)=-4
知识点
已知f(x)是奇函数,g(x)是偶函数,且f(-1)+g(1)=2,f(1)+g(-1)=4,则g(1)等于____
正确答案
解析
由题知f(-1)+g(1)= - f(1)+g(1)= 2,
f(1)+g(-1)= f(1)+ g(1)= 4.上式相加,解得g(1) = 3 。
知识点
17.设等比数列




正确答案
解析
设
解得

当

当
知识点
已知函数f(x)=
正确答案
解析
知识点
传说古希腊毕达哥拉斯学派的数学家经常在沙滩上画点或用小石子表示数,他们研究过如图所示的三角形数:
将三角形数1,3,6,10,…记为数列{an},将可被5整除的三角形数按从小到大的顺序组成一个新数列{bn},可以推测:
(1)b2 012是数列{an}中的第______项;
(2)b2k-1=______.(用k表示)
正确答案
5 030;
解析
(1)由题意可得,a1=1,a2=3,a3=6,a4=10,…,a2-a1=2,a3-a2=3,a4-a3=4,…,an-an-1=n.
以上各式相加得,an-a1=2+3+…+n=

由此归纳出b2 012=a5 030.
(2)b1=a4=


归纳出b2k-1=
知识点
扫码查看完整答案与解析