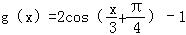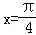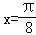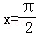- 函数y=Asin(ωx+φ)的图象变换
- 共79题
若函数f(x)=sin(x+θ)(

正确答案

解析
∵函数f(x)=sin(x+θ)的图象关于直线x=
∴

∴θ=kπ+
又0<θ<
∴θ=
知识点
将函数

所有的点的横坐标变为原来的
对应的函数解析式为( )。
正确答案
解析





知识点
将函数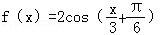
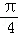
正确答案
解析
将函数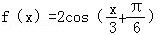
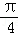
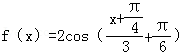
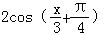
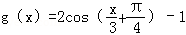
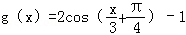
知识点
函数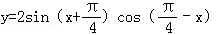
正确答案
解析
y=2sin(x+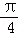
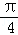
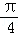

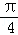
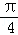
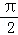
令2x=2kπ+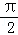
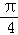
则k=1时,x=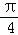
故选A
知识点
已知函数

(1)求函数
(2)若函数




正确答案
见解析。
解析
(1)



当

函数

(2)函数





即


知识点
已知函数f(x)=(sin2x+cos2x)2﹣2sin22x。
(1)求f(x)的最小正周期;
(2)若函数y=g(x)的图象是由y=f(x)的图象向右平移

正确答案
见解析
解析
解:(1)因为f(x)=(sin2x+cos2x)2﹣2sin22x=sin4x+cos4x=
所以函数f(x)的最小正周期为
(2)依题意,y=g(x)=

因为
当


当
知识点
将函数

正确答案
解析
略
知识点
已知角



正确答案
解析
略
知识点
设函数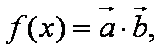
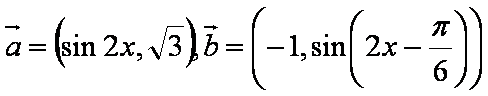
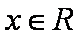
(1)求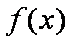
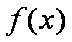
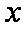
(2)将函数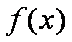
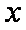
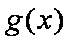
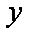
正确答案
见解析。
解析
(1)
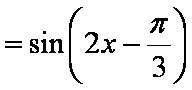
故函数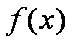
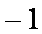
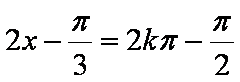
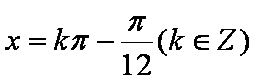
故使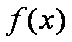
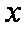
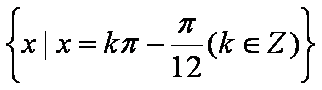
(2)由条件可得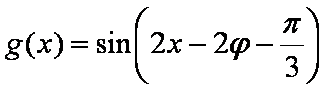
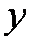
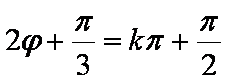
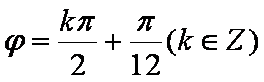
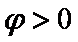
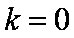
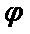
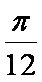
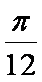
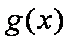
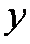
知识点
10.把函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析