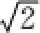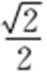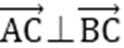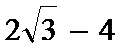8．已知O.A.B是平面上的三点，向量
A
B5
C3
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7．已知向量
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6.已知向量a，b，c满足
A
B
C
D
正确答案
解析
由
不妨设a=(2，0)，b=(1，
由(a-c)·(b-2c)=0可得(2-x)(1-2x)+(-y)(
整理得2x2-5x+2y2-
则
知识点
5.已知a，b是平面内两个互相垂直的单位向量，若向量c满足(a-c)·(b-c)=0，则|c|的最大值是（ ）
A1
B2
C
D
正确答案
解析
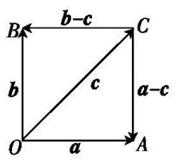
因为(a-c)·(b-c)=0，所以(a-c)⊥(b-c).
如图所示，设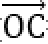
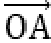
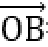
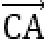
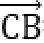
又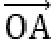
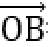
当且仅当OC为圆的直径时，|c|最大，且最大值为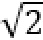
知识点
8.若a，b，c均为单位向量，且a·b=0，(a－c)·(b－c)≤0，则|a+b－c|的最大值为（ ）
A
B1
C
D2
正确答案
解析
设a=(1，0)，b=(0，1)，c=(x，y)，则x2+y2=1，
a－c=(1－x，－y)，b－c=(－x，1－y)，
则(a－c)·(b－c)=(1－x)(－x)+(－y)(1－y)=x2+y2－x－y=1－x－y≤0，即x+y≥1，
又a+b－c=(1－x，1－y)，
∴|a+b－c|=
∵c=(x，y)对应的点在
∴|a+b－c|的最大值为1.
知识点
21．已知向量a、b、c是同一平面内的三个向量，其中a＝（1，2）．
（1）若|c|＝2
（2）若|b|＝
正确答案
（1）令c＝（x，y），则由|c|＝2
又由a∥c知，2x－y＝0②
联立①②可解得：
故c＝（2，4）或c＝（－2，－4）．
（2）由a＋2b与2a－b垂直知（a＋2b）·（2a－b）＝0，
即2a2＋3a·b－2b2＝0，∴a·b＝
即|a||b|cosθ＝
而由a＝（1，2）知|a|＝
∵θ∈[0，π]，∴θ＝π．
解析
解析已在路上飞奔，马上就到！
知识点
13．已知平面向量
正确答案
解析
分三种情况考虑：
（1）
（1）
（1）
三者比较大小后知应选
知识点
14．已知向量a=(1，
正确答案
2
解析
根据a=(1，
所以
即
考查方向
解题思路
本题考查平面向量的有关问题，
解题步骤如下：根据向量的坐标表示写出
易错点
1、向量模的求解出错；
2、向量的数量积的定义理解出错。
知识点
4．设
正确答案
解析
所以
考查方向
解题思路
由基本运算入手
易错点
考虑过多，想到向量的零向量，以及向量平行的同向和反向两种情况而误导出错
知识点
4．设向量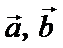
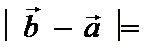
A1
B2
C-2
D
正确答案
解析
考查方向
解题思路
先使用向量减法的几何意义做
易错点
没理解向量模的 意义
知识点
扫码查看完整答案与解析