- 法拉第电磁感应定律
- 共387题
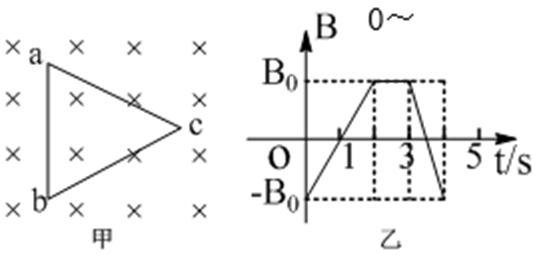
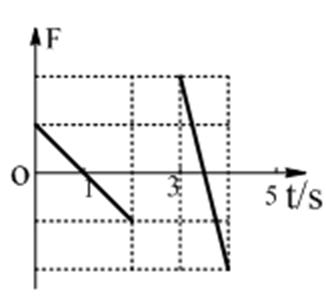
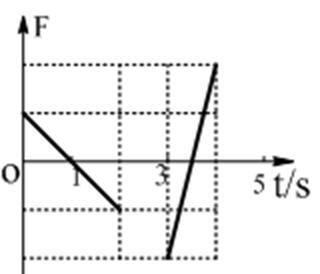
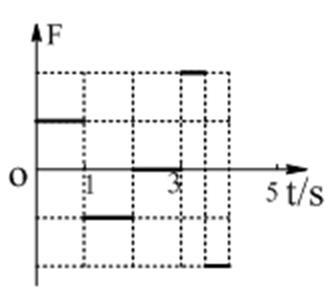
17.如图1所示,线圈abcd固定于匀强磁场中,磁场方 向垂直纸面向外,磁感应强度随时间的变化情况如图2所示。下列关于ab边所受安培力随时间变化的F-t图像(规定安培力方向向右为正)正确的是( )
正确答案
解析
由楞次定律知,由图可知感应电流的方向为adcba,根据电磁感应定律得:
根据欧姆定律得:
考查方向
法拉第电磁感应定律;安培力
解题思路
根据楞次定律和法拉第电磁感应定律判断出感应电流的方向和大小,根据左手定则判断出安培力的方向以及根据安培力的公式判断安培力大小.
易错点
本题的关键掌握楞次定律和法拉第电磁感应定律,以及安培力的大小和方向的判定.
知识点
雌三醇测定的目的是了解胎儿的
A.宫内发育情况
B.皮肤成熟情况
C.肝脏成熟情况
D.肾脏成熟情况
E.胎盘功能
正确答案
E
解析
测定孕妇体内的雌三醇是监测胎儿成熟程度的一个指标,雌三醇的前身物质来源于母体及胎儿,然后由胎盘合成,所以用来判断胎盘功能。
17.如图所示,边长为2l的正方形虚线框内有垂直于纸面向里的匀强磁场,一个边长为l的正方形导线框所在平面与磁场方向垂直,导线框的一条对角线和虚线框的一条对角线恰好在同一直线上.从t=0开始,使导线框从图示位置开始以恒定速度沿对角线方向移动进入磁场,直到整个导线框离开磁场区域.用I表示导线框中的感应电流(以逆时针方向为正).则下列表示I-t关系的图线中,正确的是( )
正确答案
解析
A、B,导线框完全进入磁场后,没有感应电流产生,故A、B均错误;
C、进入和穿出磁场过程,线框有效切割磁感线的长度变化,感应电动势和感应电流在变化,故C错误;
D、线框进入磁场过程,有效切割磁感线的长度L均匀增大,感应电动势E均匀增大,感应电流I均匀增大.穿出磁场过程,有效切割磁感线的长度L均匀减小,感应电动势E均匀减小,感应电流I均匀减小,两个过程电流方向相反,故D正确.
考查方向
右手定则;导体切割磁感线时的感应电动势
解题思路
根据右手定律结合线框运动过程分析判断产生的感应电流的大小与方向,然后逐项分析.
易错点
理解产生感应电流的条件是关键,结合特殊位置,及导线框的运动过程分析解答.
知识点
周女士,头晕乏力半年,手足关节痛3年余,查体双手指5肌肉萎缩,手指向尺侧偏,X线显示关节腔变窄,关节半脱位,血沉380mm/h,此患者最可能的诊断是
A.退行性骨关节病
B.类风湿性关节炎
C.先天性关节畸形
D.风湿性关节炎
E.系统性红斑狼疮
正确答案
B
解析
此题考察类风湿性关节炎诊断,主要根据临床表现结合相关检查。
18.如图甲所示,正三角形导线框abc固定在磁场中,磁场方向与线圈平面垂直,磁感应强度B随时间变化的关系如图乙所示。t=0时刻磁场方向垂直纸面向里,在0~4s时间内,线框ab边所受安培力F随时间t变化的关系(规定水平向左为力的正方向)可能是下图中的 ( )
正确答案
解析
A B、3t0-4t0内,感应电动势为: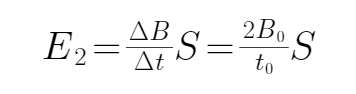
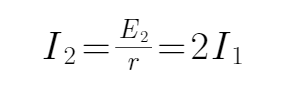
C D、 0-2t0时间内,感应电动势为:
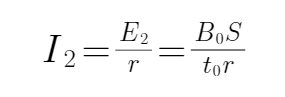
考查方向
电磁感应中的力
解题思路
先由法拉第电磁感应定理和欧姆定律求出感应电流I,然后由
易错点
磁通量的变化量计算
知识点
14.如图甲是法拉第在1831年做成的世界上第一台铜盘发电机实物图,图乙是这个铜盘发电机的示意图,两块铜片C、D分别与转动轴和铜盘的边缘接触,转动轴穿过铜盘中心且与磁场平行。转动铜盘就可以使闭合电路获得电流。若图中铜盘半径为r,匀强磁场的磁感应强度为B,回路总电阻为R,顺着磁场看铜盘顺时针转动的角速度为ω,以下说法正确的是( )
.
正确答案
解析
A、将铜盘看成若干条过圆心的棒,根据右手定则可知,铜盘上感应电流的方向从C到D,故A错误;
B、铜盘转动产生的感应电动势相当于长度为r的金属杆绕其中一个端点匀速转动则产生电动势;
即


C、铜盘转动切割磁感线,从而产生感应电动势,并不是穿过铜盘的磁通量变化,因此自由电子不随铜盘一起运动形成涡电流,故CD错误;
故选:B.
考查方向
法拉第电磁感应定律
解题思路
由右手定则可明确电流的方向;根据转动切割产生的电动势公式可求得电动势,由欧姆定律求解电流的大小;当穿过铜盘磁通量发生变化时,则会产生感应电动势,形成涡流,从而即可求解.
易错点
右手定则与楞次定律的区别
知识点
诊断前置胎盘较安全可靠的方法是
A.放射线检查
B.B型超声检查
C.肛门检查
D.化验检查
E.阴道检查
正确答案
B
解析
前置胎盘基本异常发生在胎盘位置较低,低于胎儿先露部。在检查时一定注意不能增加其出血的可能性,肛门检查和阴道检查可以增加出血的可能,化验检查不能发现其位置问题,放射性检查不适合孕妇使用,只有B超检查不增加其出血可能,同时可以达到确定胎盘位置的目的。
患者在甲状腺大部切除手术后一回到病房,护士就要求其回答问题,目的是为了评估患者有无
A.意识障碍
B.神经损伤
C.麻醉清醒
D.记忆受损
E.痰液阻塞
正确答案
B
解析
手术中若损伤病人的喉上神经外支可出现声调降低,损伤一侧喉返神经可出现声音嘶哑,因此通过与病人交谈可以评估有无神经损伤。
许多电磁现象可以用力的观点来分析,也可以用动量、能量等观点来分析和解释。
30.如图1所示,足够长的平行光滑金属导轨水平放置,导轨间距为L ,一端连接阻值为R的电阻。导轨所在空间存在竖直向下的匀强磁场,磁感应强度为B。质量为m、电阻为r的导体棒MN放在导轨上,其长度恰好等于导轨间距,与导轨接触良好。在平行于导轨、大小为F的水平恒力作用下,导体棒从静止开始沿导轨向右运动。
a ,当导体棒运动的速度为v时,求其加速度a的大小;
b,已知导体棒从静止到速度达到稳定所经历的时间为t,求这段时间内流经导体棒某一横截面的电荷量q.
31.在如图2所示的闭合电路中,设电源的电动势为E,内阻为r,外电阻为R,其余电
阻不计,电路中的电流为I。请你根据电动势的定义并结合能量转化与守恒定律证明:
正确答案
(1) a.
b.
解析
(1)a.当导体棒运动的速度为v时,电路中的感应电动势为
电流为
导体棒所受的安培力为
根据牛顿第二定律可得: 
联立①②③④式可得: 
b.设导体棒运动稳定的速度为vm,令⑤式中的
可得:
设某段极短的时间


其中, 
联立⑥⑦⑧

考查方向
1、考查电磁感应中导体棒切割磁感线产生的感应电动势
2、考查导体棒在磁场中的安培力公式
3、考查牛顿第二定律
解题思路
1、首先根据感应电动势的基本公式,求出导体切割磁感线的感应电动势;
2、根据电动势与电流的关系求出感应电流的大小;
3、再根据安培力的公式求出安培力的大小;
4、最后根据牛顿第二运动定律求解加速度。
易错点
1、运用牛顿第二运动定律时,容易忽略合外力F合力=ma
正确答案
(2)
解析
(2)根据电动势的定义有:
在时间t 内通过电路的电荷量为:q=It ⑩
根据能量守恒定律,非静电力做的功应该等于内外电路产生焦耳热的总和。


联立⑨⑩ 式可得:EIt = I2Rt+I2rt
整理后可得: 
考查方向
1、考查电动势的定义:在数值上,等于非静电力将单位正电荷从电源的负极通过电源内部移送到正极时所做的功, 
2、考查能量守恒及电路中焦耳热的基本公式。
解题思路
1、根据电流的定义表达出一定时间通过导体的电流的表达式;
2、根据能量守恒定律,求出非静电力所做的功;
3、再根据电动势的定义写出电动势的表达式:
易错点
1、对电动势的定义不熟悉。
2、对能量的转移分析不透彻。
12.如图(a)为一研究电磁感应的实验装置示意图,其中电流传感器(电阻不计)能将各时刻的电流数据实时通过数据采集器传输给计算机,经计算机处理后在屏幕上同步显示出I-t图像。平行且足够长的光滑金属轨道的电阻忽略不计,左侧倾斜导轨平面与水平方向夹角θ=30°,与右侧水平导轨平滑连接, 轨道上端连接一阻值R=0.5Ω的定值电阻,金属杆MN的电阻r=0.5Ω,质量m=0.2kg,杆长L=1m跨接在两导轨上。左侧倾斜导轨区域加一垂直轨道平面向下的匀强磁场,右侧水平导轨区域也加一垂直轨道平面向下的匀强磁场,磁感应强度大小都为B= 1.0T, 闭合开关S,让金属杆MN从图示位置由静止开始释放,其始终与轨道垂直且接触良好,此后计算机屏幕上显示出金属杆在倾斜导轨上滑行过程中的I-t图像,如图(b)所示。 ( g取10m/s2)
(1)求金属杆MN在倾斜导轨上滑行的最大速率;
(2)根据计算机显示出的I-t图像可知,当t=2s时,I=0.8A,0-2s内通过电阻R的电荷量为1.0C, 求0-2s内在电阻R上产生的焦耳热;
(3)金属杆MN在水平导轨上滑行的最大距离。
正确答案
(1)1m/s
(2)0.468J
(3)0.2m
解析
(1)当导体棒切割磁感线运动速率为v时,E=BLv ①
此时由闭合电路欧姆定律可知:I=
安培力的大小为:FA=BIL ③
由①②③联立解得速率为v时的安培力为FA=
导体棒向下滑行的过程中速度为v时,由牛顿第二定律有:mgsinθ-FA=ma
所以,导体棒做加速度减小,速度增大的减速运动,由I-t图线可知,当金属杆达到最大速率即匀速下滑时,加速度a=0,代入题给数据解得vm=1m/s
(2)2s末,杆的电流大小I2s=0.8A,由①、②联立解得此时速度v2s=0.8m/s
q=
代入数据解得x=1m
0~2s内,对整个系统由能量守恒定律有:mgxsinθ=
再由闭合电路欧姆定律可知QR=
(3)导体棒在水平轨道上从最大速率到静止的过程中,对导体棒由动量定理有:-IA=0-mvm-Blq'=0- mvm即q'=
由④类比可知,导体棒从最大速率至最终停止的过程中xm=0.2m
考查方向
解题思路
(1)由平衡条件求出滑行的最大速率;
(2)I-t图象与坐标轴所围成图形的面积等于通过电阻的电荷量;由能量守恒定律求出焦耳热;
(3)由动能定理解出运动的位移。
易错点
① 电流传感器读出的数据是干路中的电流;
② 导体棒切割磁感线运动的“闭环求解”方法:即 E→I→F安→F合→动力学、能量观点、动量观点解决问题的“套路”;
③ 倾斜导轨中能量守恒定律用“减小量”+“外部影响”=“增加量”方式更易求解。
知识点
扫码查看完整答案与解析