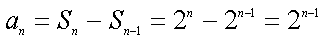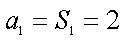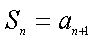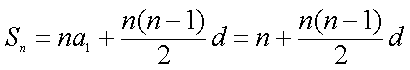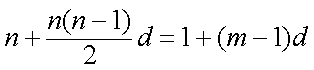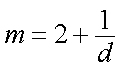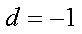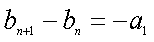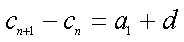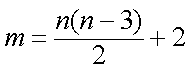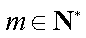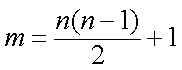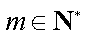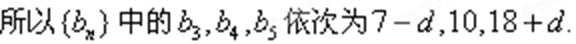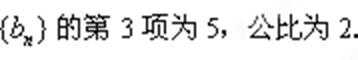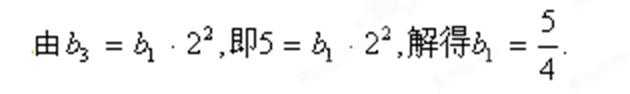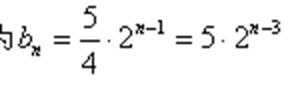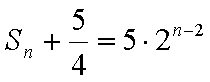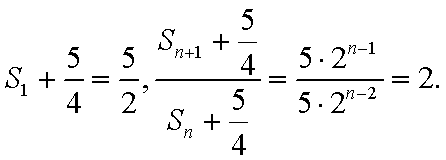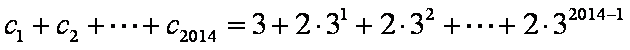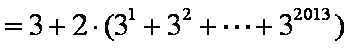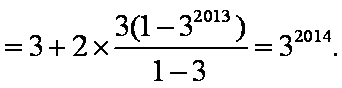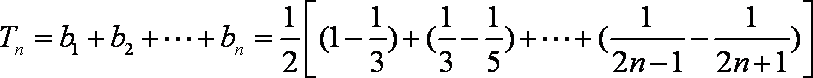- 数列
- 共2062题
设各项均为正整数的无穷等差数列{an},满足a54=2014,且存在正整数k,使a1,a54,ak成等比数列,则公差d的所有可能取值之和为 。
正确答案
126
解析
∵a54=2014,∴a1+53d=2014,
∴
∴a1是53的倍数,
∵a1,a54,ak成等比数列,
∴a542=a1ak=2×2×19×19×53×53
(1)若a1=53,53+53d=2014,d=37,
(2)若a1=2×53,106+53d=2014,d=36,
(3)若a1=4×53,212+53d=2014,d=34
(4)a1=1007,1007+53d=2014,53d=1007,d=19
∴公差d的所有可能取值之和为37+36+34+19=126。
知识点
设数列






(1)求数列
(2)当m=1时,求
(3)设





正确答案
见解析。
解析
(1)由已知




所以数列





②-①得
所以

(3)
因为


注意到,当n为奇数时,


所以


对于任意的正整数n都有
所以
知识点
已知单调递增的等比数列{aBnB}满足:aB2B+aB3B+aB4B=28,且aB3B+2是aB2B,aB4B的等差中项。
(1)求数列{aBnB}的通项公式;
(2)若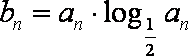
正确答案
见解析
解析
(1)设等比数列{an}的首项为a1,公比为q。
依题意,有2(a3+2)=a2+a4,代入a2+a3+a4=28,
可得a3=8,∴a2+a4=20,…………………2分
所以解之得或………………4分
又∵数列{an}单调递增,所以q=2,a1=2,
∴数列{an}的通项公式为an=2n。 ……………………6分
(2)因为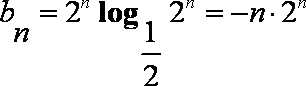
所以Sn=-(1×2+2×22+…+n·2n),
2Sn=-[1×22+2×23+…+(n-1)·2n+n·2n+1],
两式相减,得
Sn=2+22+23+…+2n-n·2n+1=2n+1-2-n·2n+1,………………10分
要使Sn+n·2n+1>50,即2n+1-2>50,即2n+1>52。
易知:当n≤4时,2n+1≤25=32<52;当n≥5时,2n+1≥26=64>52,故使
Sn+n·2n+1>50成立的正整数n的最小值为5. …………………………13分
知识点
已知函数f(x)=x2-ax+b(a,b∈R)的图像经过坐标原点,且


(1)求数列{
(2)若数列{




正确答案
见解析。
解析
(1)∵
由


∴


∵


(2)由

∴
∴


∴
知识点
设数列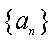
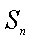
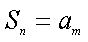
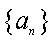
(1)若数列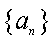
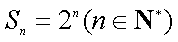
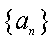
(2)设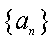
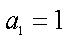
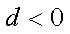
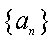
(3)证明:对任意的等差数列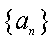
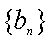
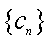
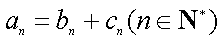
正确答案
见解析。
解析
(1)当
当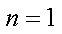
∴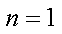
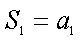

∴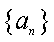
(2)
对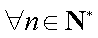
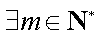
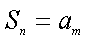
取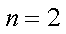
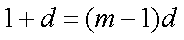
∵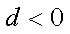
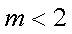
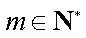
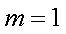
(3)设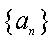
令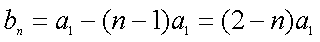
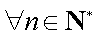
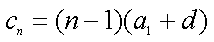
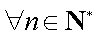
则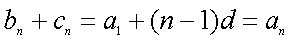
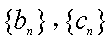
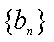
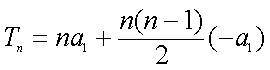
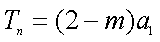
当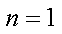
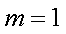
当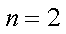
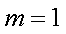
当
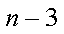
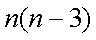
因此对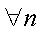
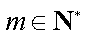
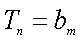
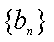
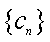
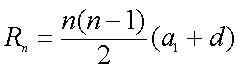
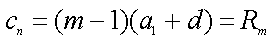
∵对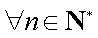
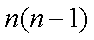
即对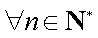
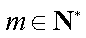
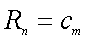
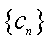
因此命题得证.
知识点
设各项均为正数的数列



(1)若λ = 1,求数列
(2)求λ的值,使数列
正确答案
见解析。
解析
(1)若λ = 1,则

又∵

∴
化简,得
∴当

② ①,得


∵当n = 1时, 
∴数列{an}是首项为1,公比为2的等比数列, an = 2n1(
(2)令n = 1,得

要使数列

当λ = 0时,

当n≥2时,
整理,得

从而
化简,得

综上所述,

所以λ = 0时,数列
知识点
成等差数列的三个正数的和等于15,并且这三个数分别加上2、5、13后成为等比数列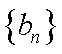
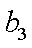
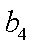
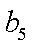
(1) 求数列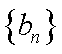
(2) 数列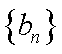
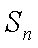
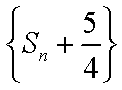
正确答案
见解析
解析
(1) 解:设成等差数列的三个正数分别为a-d,a,a+d
依题意,得a-d+a+a+d=15,解得a=5
依题意,有(7-d)(18+d)=100,解得d=2或d=-13(舍去)
故
所以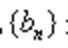
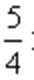
其通向公式为
(2)数列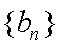
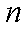
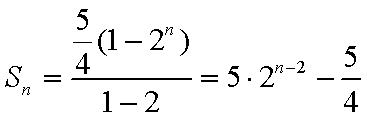
所以
因此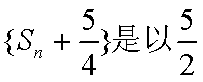
知识点
已知集合









(1)求数列
(2)若数列

求
正确答案
见解析。
解析
(1)由题设知: 集合





由此可得,对任意的



设等差数列


因为

由于


所以

所以数列


(2)
于是有

知识点
已知



(1)求数列
(2)记数列





正确答案
见解析
解析
(1)由题,设


由

即




所以数列

(2)由(1)得,

则

由

知识点
如图,在底面是矩形的四棱锥P—ABCD中,PA⊥面ABCD,E是PD的中点.
(1)求证:平面PDC⊥平面PDA;
(2)求几何体P—ABCD被平面ACE分得的两部分的体积比
正确答案
见解析。
解析
(1)∵

∴
∵四边形ABCD是矩形.
∴

又∵CD

(2)由已知

知识点
已知公差不为0的等差数列


(1)求数列
(2)设




正确答案
(1)
解析
解析:(1)设
由



联立①②得
故
(2)∵
∴
由
令

知识点
在等差数列


(1)求数列
(2)设数列





正确答案
见解析
解析
(1)设等差数列

依题意 

所以 

所以数列

(2)由数列


得 

所以 
所以

从而当

当

知识点
已知各项均为证书的数列





(1)求数列
(2)若


正确答案
(1)
解析
解析:(1)由题意知
当

当

两式相减得

∴数列


(2)由

所以,
所以数列


知识点
已知等差数列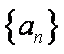
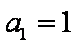
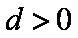
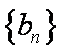
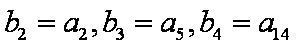
(1)求数列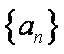
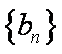
(2)设数列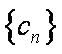
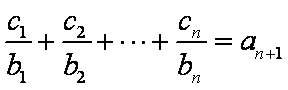
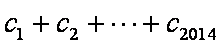
正确答案
见解析。
解析
(1)∵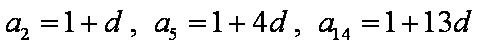
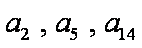
∴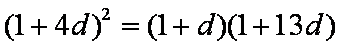
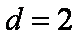
∴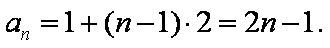
又∵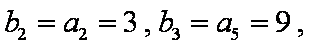
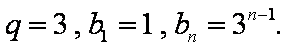
(2)∵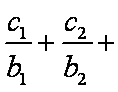
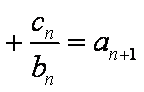
∴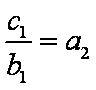
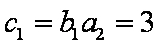
又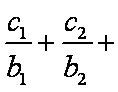
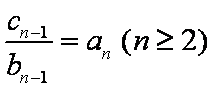
①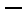
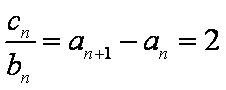
∴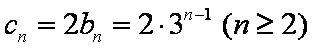
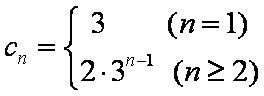
则
知识点
记数列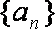
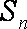
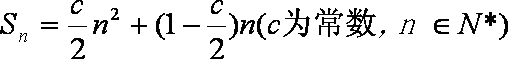
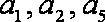
(1)求c的值;
(2)设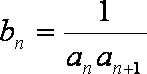
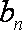
正确答案
见解析
解析
(1)由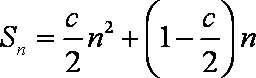
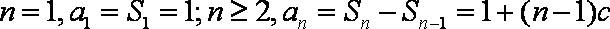
故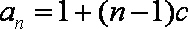
而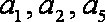
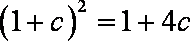
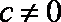
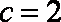
(2)由(1)知,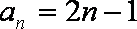
∴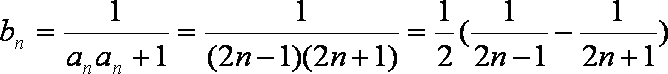
∴

知识点
扫码查看完整答案与解析