- 数列
- 共2062题
已知等差数列


17.求
18.设等比数列




正确答案
(Ⅰ)
解析
试题分析:(Ⅰ)利用等差数列的通项公式,将




(Ⅰ)设等差数列

因为

又因为


所以

考查方向
解题思路
解本题需要掌握的知识点是等差数列的通项公式,即等差数列的通项公式:
易错点
等差数列首相及公差的计算
正确答案
(Ⅰ)



解析
试题分析:(Ⅱ)先利用第一问的结论得到









(Ⅱ)设等比数列

因为

所以

所以
由

所以


考查方向
解题思路
解本题需要掌握的知识点是等比数列的通项公式,即等比数列的通项公式:
易错点
等比数列项数的判断
某超市随机选取
甲
乙
丙
丁
√
×
√
√
×
√
×
√
√
√
√
×
√
×
√
×
√
×
×
×
×
√
×
×
19.估计顾客同时购买乙和丙的概率;
20.估计顾客在甲、乙、丙、丁中同时购买
21.如果顾客购买了甲,则该顾客同时购买乙、丙、丁中那种商品的可能性最大?
正确答案
(Ⅰ)0.2.
解析
试题分析:(Ⅰ)由统计表读出顾客同时购买乙和丙的人数
(Ⅰ)从统计表可以看出,在这


考查方向
解题思路
(1)从统计表可得,在这1000名顾客中,同时购买乙和丙的有200人,从而求得顾客同时购买乙和丙的概率.
易错点
概率与频率的关系
正确答案
(Ⅱ)0.3.
解析
试题分析:(Ⅱ)先由统计表读出顾客在甲、乙、丙、丁中同时购买

(Ⅱ)从统计表可以看出,在在这





考查方向
解题思路
根据在甲、乙、丙、丁中同时购买3种商品的有300人,求得顾客顾客在甲、乙、丙、丁中同时购买3种商品的概率.
易错点
互斥事件概率加法公式
正确答案
(Ⅲ)同时购买丙的可能性最大.
解析
试题分析:(Ⅲ)由统计表读出顾客同时购买甲和乙的人数为


(Ⅲ)与(Ⅰ)同理,可得:
顾客同时购买甲和乙的概率可以估计为
顾客同时购买甲和丙的概率可以估计为
顾客同时购买甲和丁的概率可以估计为
所以,如果顾客购买了甲,则该顾客同时购买丙的可能性最大.
考查方向
解题思路
在这1000名顾客中,求出同时购买甲和乙的概率、同时购买甲和丙的概率、同时购买甲和丁的概率,从而得出结论.
易错点
概率的计算
5.设




正确答案
解析
由

考查方向
解题思路
本题解答过程中用到了的等差数列的一个基本性质即等差中项的性质,利用此性质可得
易错点
等差中项的性质的正确应用要注意下标关系
知识点
3. 设a=0.6


正确答案
解析
由y=0.6




考查方向
解题思路
利用函数的单调性求解,需要结合指数函数底数的两种不同取值情况讨论.
易错点
指数函数的性质、指数函数底数的两种不同取值情况的讨论
知识点
8.已知





正确答案

解析
设公差为


解得


考查方向
解题思路
根据等差数列的通项以及求和列出方程组,求出基本量然后求特定项。
易错点
列方程求基本量致误
知识点
5.已知等差数列



正确答案
解析
由


考查方向
解题思路
由

易错点
本题易运算上出错。
知识点
2.在等差数列



正确答案
解析
由

考查方向
解题思路
根据两个已知条件列方程组,即可求出公差d。
易错点
对等差数列的通项公式及求和公式不熟悉导致出错。
知识点
14.已知数列



正确答案
-1
解析
因为
考查方向
解题思路
先写出前几项,然后找到规律,进而求解
易错点
找不出前n项和和数列通项的关系
知识点
3.设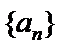
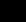
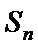
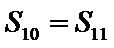
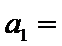
正确答案
解析
由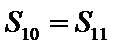
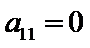
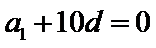
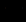
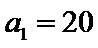
考查方向
解题思路
由已经计算出第11项为0,然后利用公差算出首项。
易错点
不会转化已知条件。
知识点
3.在等差数列{



正确答案
解析
由



考查方向
解题思路
根据已知条件来求,将式子全部化为只含公差和首项的方程,最后即可得到要求的值。
易错点
不会根据已知条件来求。
知识点
4.等差数列




正确答案
解析
因为





考查方向
解题思路
由已知
易错点
对等差数列的前n项和公式不熟悉导致出错。
知识点
18. 已知数列


(Ⅰ)求

(Ⅱ)设



正确答案
(1)


解析
试题分析:本题属于等差数列及数列的求和,
(1)直接利用公式来解答;
(2)先利用裂项相消法求出
(Ⅰ)设数列


由

所以

(Ⅱ)可得

由于

即

考查方向
解题思路
本题考查等差数列及数列的求和,解题步骤如下:(1)直接利用公式来解答;(2)先利用裂项相消法求出
易错点
第二问求和不晓得使用裂项相消法去做。
知识点
10. 数列




正确答案
解析
设数列

所以

考查方向
解题思路
先求出公差d,再根据等差数列的性质求出a11
易错点
对等差数列的性质运用错误
知识点
已知等差数列



18. 求
19. 设



正确答案
见解析
解析
(Ⅰ)设等差数列



解得
考查方向
解题思路
根据

易错点
主要易错于公比q=1的判断,
正确答案
见解析
解析
(Ⅱ)






考查方向
解题思路
利用等比数列的判定得到数列是等比数列
易错点
主要易错于公比q=1的判断,
14.已知{

正确答案
-1
解析
考查方向
解题思路
1)使用等差数列通项公式使用a1和d表示
2)使用等比中项公式得到关系式
易错点
主要易错于计算出错
知识点
扫码查看完整答案与解析























