数列_章节学习_百度题库

1

题型：填空题

|

填空题 · 5 分

11. 若数列是正项数列，且则___________

正确答案

解析

知识点

等差数列的判断与证明等差数列的前n项和及其最值

1

题型：简答题

|

简答题 · 12 分

19．已知为等差数列，且，。

（1）求数列的通项公式；

（2）记的前项和为，若．．成等比数列，求正整数的值。

正确答案

（1）由，可得：即

代入，可得：

（2）

化简可得：解得（舍去）

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项等差数列的基本运算等差数列的前n项和及其最值等差数列与等比数列的综合

1

题型：单选题

|

单选题 · 5 分

8．已知为等差数列，若，则（）

A24

B27

C15

D54

正确答案

B

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的基本运算等差数列的性质及应用等差数列的前n项和及其最值

1

题型：填空题

|

填空题 · 5 分

11．已知数列的前项和，则其通项公式____________。

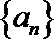
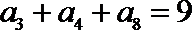
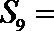
正确答案

2n-10

解析

解析已在路上飞奔，马上就到！

知识点

由递推关系式求数列的通项公式等差数列的判断与证明等差数列的前n项和及其最值

1

题型：单选题

|

单选题 · 5 分

4.已知是等差数列，，则该数列前10项和等于（）

A64

B100

C110

D120

正确答案

B

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的基本运算等差数列的前n项和及其最值

1

题型：单选题

|

单选题 · 5 分

8.在中，已知前项和则（）

A69200

B1400

C1415

D1385

正确答案

B

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的基本运算等差数列的判断与证明等差数列的前n项和及其最值

1

题型：单选题

|

单选题 · 5 分

9.已知等差数列共有10项，其中奇数项之和15，偶数项之和为30，则其公差是（）

A5

B4

C3

D2

正确答案

C

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的基本运算等差数列的性质及应用等差数列的前n项和及其最值

1

题型：简答题

|

简答题 · 13 分

19．已知为等差数列，且，数列的前项和为，且。

（1）求数列的通项公式；

（2）若，为数列的前项和，求证：。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由an与Sn的关系求通项an等差数列的基本运算等差数列的前n项和及其最值错位相减法求和数列与不等式的综合

1

题型：单选题

|

单选题 · 5 分

9．一个样本容量为20 的样本，它的数据组成一个公差不为0 的等差数列，若，前4项的和,则这个样本的平均数和中位数分别是（）

A22，23

B23，22

C23，23

D23，24

正确答案

C

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的基本运算等差数列的前n项和及其最值众数、中位数、平均数

1

题型：单选题

|

单选题 · 5 分

2．在等差数列中，，则此数列的前项的和等于（）

A

B

C

D

正确答案

D

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的性质及应用等差数列的前n项和及其最值

1

题型：单选题

|

单选题 · 5 分

4．等差数列中，若，则（）

A

B

C1

D

正确答案

C

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的基本运算等差数列的前n项和及其最值

1

题型：单选题

|

单选题 · 5 分

10．已知是等差数列的前n项和，若，则的值为（）

A

B

C

D

正确答案

D

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的基本运算等差数列的性质及应用等差数列的前n项和及其最值

1

题型：填空题

|

填空题 · 4 分

5．设数列．均为等差数列，且公差均不为，，则__________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的基本运算等差数列的前n项和及其最值数列的极限

1

题型：简答题

|

简答题 · 12 分

18.在等差数列中，，、、成等比数列，求数列的前n项和.

正确答案

解：设等差数列的公差为d.

因为、、成等比数列，所以.

所以.

所以 ①

因为

所以 ②

由①②得：或

若，则；

若，则.

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的基本运算等差数列的前n项和及其最值等比数列的性质及应用

1

题型：简答题

|

简答题 · 16 分

21．已知公比为的无穷等比数列各项的和为9，无穷等比数列各项的和为。

（1）求数列的首项和公比；

（2）对给定的，设是首项为，公差为的等差数列，求的前2007项之和；

（3）设为数列的第项，：求的表达式，并求正整数，使得存在且不等于零。

正确答案

（1）依题意可知，。

（2）由（1）知，，所以数列的的首项为，公差，

，即数列的前项之和为。

（3）===；

；

=，

当时，=－，当时，=0，所以。

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的基本运算等差数列的前n项和及其最值等比数列的基本运算数列的极限

热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点