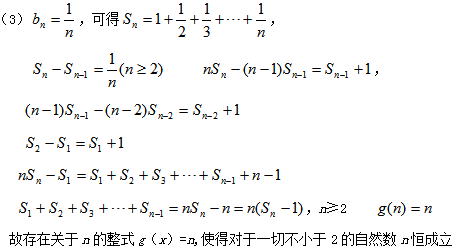- 数列
- 共2062题
13.已知等差数列





正确答案
7
解析
解析已在路上飞奔,马上就到!
知识点
17.数列








正确答案

解析
解析已在路上飞奔,马上就到!
知识点
6. 若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知等差数列


(1)求数列
(2)求使不等式

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.设递增等差数列






(I)求数列
(II)求数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.设数列
(I)求数列
(II)是否存在正整数n使得

正确答案
解:(I)




(II)

解析
解析已在路上飞奔,马上就到!
知识点
19.已知数列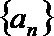
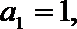
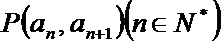
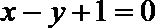
(1)求数列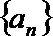
(2)若函数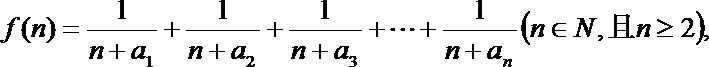
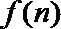
(3)设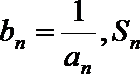
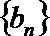
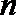
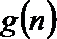
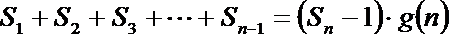
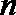
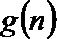
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知数列

正确答案
解析
当n=1时,a1=S1=9;
当n≥2时,an=Sn-Sn-1=11-2n,由于n=1时,a1=9也满足11-2n,因此an=11-2n.
(1)当n>5时,Tn=|a1|+|a2|+…+|an|=-Sn+2S5=n2-10n+50,
(2)当n≤5时,Tn=|a1|+|a2|+…+|an|=-(a1+a2+…+an)=10n-n2,
综合(1)(2),得Tn=
知识点
14.已知数列

正确答案
解析
当n=1时,a1=S1=9;
当n≥2时,an=Sn-Sn-1=11-2n,由于n=1时,a1=9也满足11-2n,因此an=11-2n.
(1)当n>5时,Tn=|a1|+|a2|+…+|an|=-Sn+2S5=n2-10n+50,
(2)当n≤5时,Tn=|a1|+|a2|+…+|an|=-(a1+a2+…+an)=10n-n2,
综合(1)(2),得Tn=
知识点
8.已知等差数列{an}的前n项和为Sn,若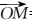
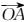
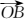
正确答案
2015
解析
若O、A、B、M为平面内四点,则A、B、M三点在一条直线上,当且仅当存在一对实数m、n,使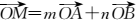
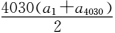
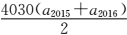
知识点
16.已知等差数列{an}的前n项和为Sn,若=a100+a101,且A、B、C三点共线(该直线不过点O),则S200等于________.
正确答案
100
解析
由条件可得a100+a101=1,即a1+a200=1,从而S200=100.故填100.
知识点
4.在等差数列{



正确答案
解析
由





考查方向
解题思路
根据题目条件先求出
易错点
没有记清楚等差数列的相关性质是导致本题出错的主要原因。
知识点
18. 设数列

(1)求数列

(2)是否存在正整数n,使得
正确答案
(1)
(2)
解析
本题属于三角函数的图像与性质及正余弦定理的综合应用问题,属于简单题,只要掌握相关函数的知识,即可解决本题,解析如下:
解:(1)
所以
两式相减得:
即

所以

所以
所以
所以
所以
所以

考查方向
本题考查了数列的相关知识点,属于简单题。
易错点
相关知识点不熟悉导致出错。
知识点
扫码查看完整答案与解析