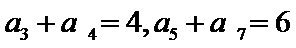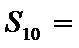- 数列
- 共2062题
17.等差数列{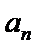
(I)求{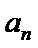
(II)设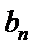
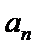
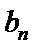
正确答案
知识点
5.小敏打开计算机时,忘记了开机密码的前两位,只记得第一位是M,I,N中的一个字母,第二位是1,2,3,4,5中的一个数字,则小敏输入一次密码能够成功开机的概率是()
正确答案
知识点
17.等差数列{
(I)求{
(II)设


正确答案
(Ⅰ)
解析
(Ⅰ) 根据等差数列的性质求




试题解析:(Ⅰ)设数列


所以

(Ⅱ)由(Ⅰ)知
当n=1,2,3时,
当n=4,5时,
当n=6,7,8时,
当n=9,10时,
所以数列

考查方向
解题思路
(I)用基本量法,根据等差数列通项公式
易错点
求解本题会出现以下错误:①对“

知识点
设数列






且当

24.求
25.证明:
26.求数列
正确答案
(1)
解析
(1)当


考查方向
解题思路
(1)令









易错点
证明等比数列时,不能写出几项去验证,而是要利用定义去证明。
正确答案
(2)证明见解析;
解析
(2)因为











考查方向
解题思路
(1)令









易错点
证明等比数列时,不能写出几项去验证,而是要利用定义去证明。
正确答案
(3)
解析
(3)由(2)知:数列


即






考查方向
解题思路
(1)令









易错点
证明等比数列时,不能写出几项去验证,而是要利用定义去证明。
已知数列


21.求数列
22.设
正确答案
解析
(1)设数列






考查方向
解题思路
运用从一般到特殊的处理方法,准确确定等差数列的通项公式。
正确答案
解析
(2)由(1)知,

得
考查方向
解题思路
对所得数学式子准确地变形,应用“错位相减法”求和。
易错点
错位相减后求和时,弄错数列的项数,或忘记从

17.已知


(I)求
(II)求
正确答案
解:(1) ∵ anbn+1+bn+1=nbn ∴ n=1时 a1·b2+b2=b1
∴ a1· 
∴ an=a1+(n-1)·d=2+3(n-1) ∴ an=3n-1
(2)由①知

∴ (3n-1)bn+1+bn+1=nbn ∴ bn+1= 
∴ 设{bn}构成以1为首项,公比为 
∴ 设{bn}前n项和Sn,则Sn
知识点
14.无穷数列{an}由k个不同的数组成,Sn为{an}的前n项和.若对任意的

正确答案
4
知识点
已知



22.求

23.设

正确答案


解析
试题分析:列出关于q与d的方程组,通过解方程组求出q,d,即可确定通项;设









考查方向
解题思路
近几年高考试题中求数列通项的题目频频出现,尤其对等差、等比数列的通项考查较多,解决此类 问题要重视方程思想的应用.
易错点
准确求解方程
正确答案
解析
试题分析:用错位相减法求和.
由(I)有


两式相减得
所以
考查方向
解题思路
错位相减法求和也是高考考查频率较高的一类方法,从历年考试情况来看,这类问题,运算失误较多,应引起考生重视.
易错点
错位相减法相减时项的对应关系
3.已知等差数列
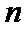
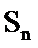
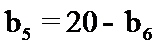
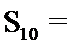
正确答案
解析
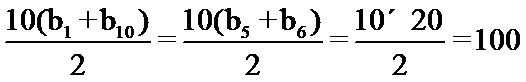
考查方向
解题思路
利用等差数列的求和公式表示出前10项的和,再利用等差数列的性质即可解出。
易错点
不会利用等差数列的性质来求解。
知识点
5.设Sn是等差数列{an}的前n项和,若a1+a3+a5=3 ,则S5 = (
正确答案
解析
根据关系式a1+a3+a5=3,得到a1+2d=1,,S5=5a1+10d,所以S5=5(a1+2d)=5,所以本题选A
考查方向
本题主要考查等差数列项数和项之间的关系,属于中档题,是高考的热点。
解题思路
通过前三项奇数项关系式,求出等差数列的首项和公差,利用等差数列前n项和求和公式求解。
易错点
等差数列项数和项概念混淆。
知识点
9.已知等比数列



正确答案
解析
解:设等比数列{an}的公比是q,因为


考查方向
解题思路
设等比数列{an}的公比是q,根据题意和等比数列的通项公式列出方程,化简后求出q的值,即可求出a2
易错点
计算错误,主要是用换元法。
知识点
4.等差数列




正确答案
解析
因为





考查方向
解题思路
由已知
易错点
对等差数列的前n项和公式不熟悉导致出错。
知识点
5. 设




正确答案
解析
由等差中项性质得:
考查方向
解题思路
利用等差中项的概念,可以得到第三项,再利用前五项的和与第三项的关系可得。
易错点
利用前n项和公式,找不到前五项和和已知条件的关系。
知识点
18. 已知数列


(Ⅰ)求

(Ⅱ)设



正确答案
(1)


解析
试题分析:本题属于等差数列及数列的求和,
(1)直接利用公式来解答;
(2)先利用裂项相消法求出
(Ⅰ)设数列


由

所以

(Ⅱ)可得

由于

即

考查方向
解题思路
本题考查等差数列及数列的求和,解题步骤如下:(1)直接利用公式来解答;(2)先利用裂项相消法求出
易错点
第二问求和不晓得使用裂项相消法去做。
知识点
已知等差数列



16.求
17.设等比数列






正确答案
(Ⅰ)
解析
试题分析:(Ⅰ)由已知及等差数列的通项公式和前n项和公式可得关于数列的首项a1和公式d的二元一次方程组,解此方程组可求得首项及公差的值,从而可写出此数列的通项公式.
试题解析: (1)设

化简得
解得
故通项公式

考查方向
解题思路
本题考查等差数列的概念、通项公式及前n项的求和公式,利用方程组思想求解.本题属于基础题.
易错点
等差数列性质的运用
正确答案

解析
试题分析: (Ⅱ)由(Ⅰ)的结果可求出b1和b4的值,进而就可求出等比数列的公比,再由等比数列的前n项和公式



设


故

考查方向
解题思路
本题考查等比数列的概念、通项公式及前n项的求和公式,利用方程组思想求解.本题属于基础题.
易错点
注意运算的准确性
扫码查看完整答案与解析