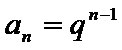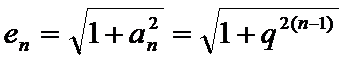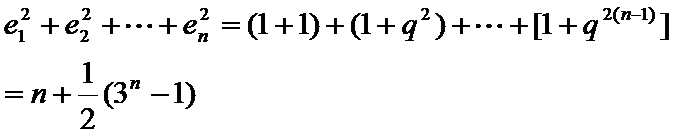- 数列
- 共2062题
15.已知


①函数

②若

③若

④若


其中正确的的序号是 ____________ .(把你认为正确的序号都填上)
正确答案
①④
解析
解析已在路上飞奔,马上就到!
知识点
19.在数列

(I)证明

(II)求

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.数列
(1)求证:数列
(2)求数列
(3)等差数列


正确答案
(1)
又
所以
数列
(2)
(3)
等差数列
设公差为
则
又

解析
解析已在路上飞奔,马上就到!
知识点
4.若数列满足

正确答案
解析
依题意可得bn+1=pbn,则数列为等比数列。又b1b2b3…b99=599,所以b50=5,故b10·b90=
知识点
19.已知数列


(1)证明:数列

(2)设

正确答案
解:(1)
(2)
解析
解析已在路上飞奔,马上就到!
知识点
8.公比不为




正确答案
解析
由









考查方向
解题思路
先根据已知条件求出首项和公比,再求和。
易错点
相关知识点不熟悉导致出错。
知识点
6.设等比数列




正确答案
63.
解析
由等比数列前n项和的性质



设等比数列{an}的首项为a1,公比为q.显然q≠1,由题意得


考查方向
解题思路
本题主要考查等比数列的基本运算,等比数列的求和。解题步骤如下:
利用公式或性质,列出等式。
正确运算,得出结果。
易错点
本题易错点是公式会弄错,运算上出现错误。
知识点
20.若数列

(1)已知数列

①求数列
②试判断数列
(2)已知数列


正确答案
(1)①
(2)略.
解析
试题分析:此题是结合等差(比)数列,给出新定义的创新试题,难度较大。在解题中要充分利用新定义的性质,合理推理,得出结论。
(1)①由an+1=2an-1,得an+1-1=2(an-1),且a1-1=1,
所以数列{an-1}是首项为1,公比为2的等比数列.
所以an-1=2n-1.
所以,数列{an}的通项公式为a n=2n-1+1.
②数列{an}不是“等比源数列”.用反证法证明如下:
假设数列{an}是“等比源数列”,则存在三项am,an,ak (m<n<k)按一定次序排列构成等比数列.
因为an=2n-1+1,所以am<an<ak.
所以an2=am·ak,得 (2n-1+1)2=(2m-1+1)(2k-1+1),即22n-m-1+2n-m+1-2k-1-2k-m=1.
又m<n<k,m,n,k∈N*,
所以2n-m-1≥1,n-m+1≥1,k-1≥1,k-m≥1.
所以22n-m-1+2n-m+1-2k-1-2k-m为偶数,与22n-m-1+2n-m+1-2k-1-2k-m=1矛盾.
所以,数列{an}中不存在任何三项,按一定次序排列构成等比数列.
综上可得,数列{an}不是“等比源数列”.
(2)不妨设等差数列{an}的公差d≥0.
当d=0时,等差数列{an}为非零常数数列,数列{an}为“等比源数列”.
当d>0时,因为an∈Z,则d≥1,且d∈Z,所以数列{an}中必有一项am>0.
为了使得{an}为“等比源数列”,
只需要{an}中存在第n项,第k项(m<n<k),使得an2=amak成立,
即[am+(n-m)d]2=am[am+(k-m)d],即(n-m)[2am+(n-m)d]=am(k-m)成立.
当n=am+m,k=2am+amd+m时,上式
所以,数列{an}为“等比源数列”.
考查方向
解题思路
本题主要考查数列的概念.等差数列.等比数列的的通项公式与求和公式.不等式的求解等基本性质.解题步骤如下:
根据已知条件构造新数列,从而求出数列的通项a n;
利用等差(比)数列的性质,和题目给出的新定义“等比源数列”进行合理的恒等变换和推理,得出解答。
易错点
不能正确理解题目中给出的新定义“等比源数列”
在判断“等比源数列”中的恒等变换时易出错。
知识点
已知等比数列








17.求

18.设数列




正确答案

解析
试题分析:本题属于数列知识的综合应用问题,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:
(1)设数列




考查方向
解题思路
(1)直接利用相关知识点求解;(2)利用裂项相消法求和.
易错点
相关知识点不熟容易处错。
正确答案

解析
试题分析:本题属于数列知识的综合应用问题,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:
由题意得:
考查方向
解题思路
(1)直接利用相关知识点求解;(2)利用裂项相消法求和.
易错点
相关知识点不熟容易处错。
6. 若



正确答案
解析
由题可知:等比数列的相邻两项相乘仍然是等比数列。
A选项不正确,C选项不正确,D选项不正确,所以选B选项。
考查方向
解题思路
代入特值计算或由等比数列的基本性质,即可得到结果。
A选项不正确,C选项不正确,D选项不正确,所以选B选项。
易错点
本题易在代特值时发生错误。
知识点
7.已知
正确答案
知识点
已知数列{an}的首项为1, Sn为数列{an}的前n项和,Sn+1=qSn+1,其中q﹥0,n∈N+
23.若a2,a3,a2+a3成等差数列,求数列{an}的通项公式;
24.设双曲线x2﹣=1的离心率为en,且e2=2,求e12+ e22+…+en2,
正确答案
(Ⅰ)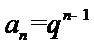
解析
(Ⅰ)由已知,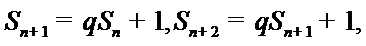

又由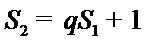
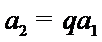
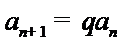
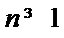
所以,数列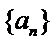
从而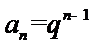
由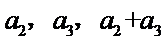
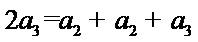
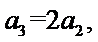
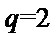
所以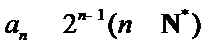
考查方向
解题思路
先利用双曲线的离心率定义得到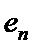
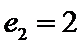
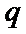
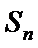
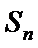
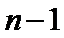
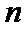
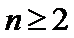
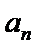

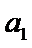
易错点
本题考查数列的通项公式、双曲线的离心率、等比数列的求和公式等基础知识,在求离心率时易错。
正确答案
(Ⅱ)
解析
(Ⅱ)由题意可得,
所以双曲线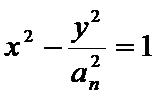
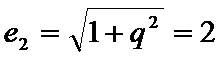
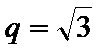
考查方向
解题思路
先利用双曲线的离心率定义得到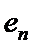
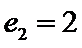
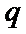
易错点
本题考查数列的通项公式、双曲线的离心率、等比数列的求和公式等基础知识,在求离心率时易错。
11. 在等比数列




正确答案
3
解析
由题可知,a5=3a1+2a3,q4=3+2q2,q2=3,则
考查方向
解题思路
表示等差数列,表示首项与公比的关系,代入即可得到结果。
易错点
本题易在表示等差数列时发生错误。
知识点
19. 设数列






(1)求证:数列

(2)令








正确答案
见解析
解析
解:(1)当


代入

而
∴数列
∴


又
(2)当



∴
故
当

若
则等式


若


∵



∴当且仅当


综上可知,当


当


考查方向
解题思路
利用

易错点
忽略n的范围的讨论。
知识点
18.在数列{an}中,a1=2,an+1=
(1)求证:
(2)求数列{an}的前n项之和Sn.
正确答案
略.
解析
试题分析:本题属于数列中的基本问题,题目的难度是逐渐由易到难.
(1)由已知得
所以
考查方向
本题考查了数列的问题.属于高考中的高频考点。
解题思路
本题考查数列问题,解题步骤如下:
(1)利用等比数列的定义证明。
(2)利用错位相减法求和。
易错点
错位相减法求和时相减的结果项数易错。
知识点
扫码查看完整答案与解析