- 数列
- 共2062题
20.已知数列


(1)求证:
(2)记


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22. 
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.等比数列



正确答案
27
解析
解析已在路上飞奔,马上就到!
知识点
18.已知数列


(1)求证:数列
(2)求数列

正确答案
(1)∵
∴
又
∴
∴数列
(2)由(1)知数列
∴
∴数列
解析
解析已在路上飞奔,马上就到!
知识点
7.已知数列{



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.数列1,1+2,1+2+22,…,1+2+22+…+2n-1,…的前n项和为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.设正项等比数列

正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
21.已知数列{an}中,a1=2,前n项和为Sn,对于任意n≥2,3Sn-4,an,
(I)求数列
(II)若数列



正确答案
(I)∵n≥2时,3Sn-4,an,2-
∴
即 
∴ 
两式相减,得

∴a2,a3,…an,…成等比数列.
∵a1=2 当n =2时,a2= 
∴a1,a2,a3,…an,…成等比数列,
∴an=2
(II)由(I)得 
∴

∵ 
∴ 
解析
解析已在路上飞奔,马上就到!
知识点
4.已知等比数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.若等比数列
_________.
正确答案
20
解析
解析已在路上飞奔,马上就到!
知识点
23.已知数列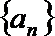
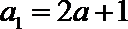
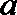
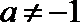
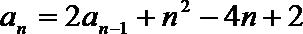
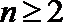
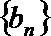
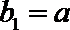
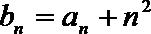
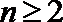
(1)证明: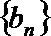
(2)设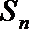
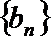
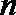
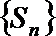
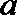
(3)当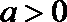
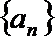
正确答案
(1)∵
∴
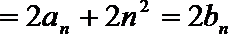
由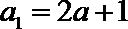
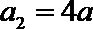
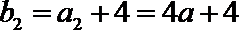
∵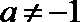
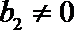
即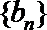
(2)
当n≥2时,
∵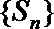
∴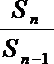
∴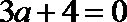
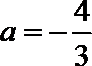
(3)由(1)知当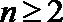
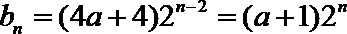
所以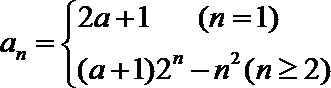
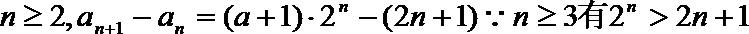
显然最小项是前三项中的一项.
当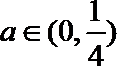
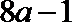
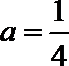
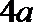
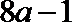
当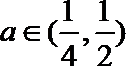
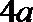
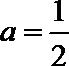
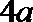
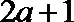
当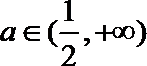
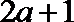
解析
解析已在路上飞奔,马上就到!
知识点
13. 已知





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.甲、乙两容器中分别盛有浓度为





(1)试用



(2)求证:数列{



(3)求出数列{

正确答案
(1)
(2)两式相减

两式相加


(3)
解析
解析已在路上飞奔,马上就到!
知识点
14.已知数列



正确答案
11
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析