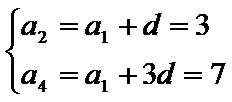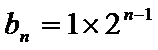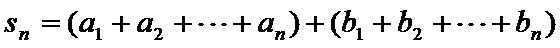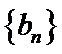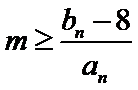- 数列
- 共2062题
3.中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还。”其意思为:“有
正确答案
解析
由题意可知

考查方向
解题思路
由已知可得等比数列的公比是1/2,前六项的和为378,可以求出首项,进一步求出第二项即可。
易错点
不会转化为等比数列来做。
知识点
14.各项均为正数的等比数列



正确答案
解析
试题分析:由




考查方向
解题思路
直接利用等比数列的通项公式进行计算。
易错点
相关知识点不熟悉导致出错。
知识点
7. 已知等比数列



正确答案
解析
由


考查方向
解题思路
由

易错点
公比的正负情况不知道。
知识点
17.已知数列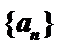
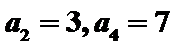
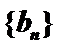
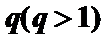
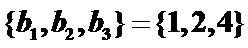
(Ⅰ)求数列

(Ⅱ)求数列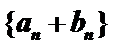
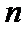
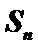
正确答案
(1)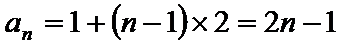
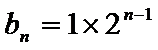
解析
试题分析:本题属于数列中的基本问题,题目的难度不大,(1)直接按照步骤来求(2)利用求和公式来解.
(Ⅰ)设等差数列的首项和公差分别为: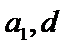
解得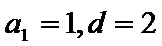

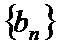
∴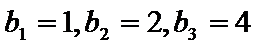
∴
(Ⅱ)
=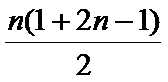
= 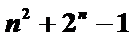
考查方向
解题思路
本题考查等差数列和等比数列以及数列的求和,解题步骤如下:
用待定系数法构造关于首项和公差公比的方程组。
等差等比的求和公式。
易错点
第2问不知道分组求和。
知识点
3.在等比数列


正确答案
解析
因为等比数列中,




考查方向
解题思路
根据等比数列的性质求出公比q的值,然后求出前五项的积
易错点
计算错误;概念理解错误
知识点
10.已知





正确答案

解析
试题分析:利用题中给出条件求出首项和公差的关系,列方程求出值即可。
由


即



即

故答案为
考查方向
解题思路
运用等比数列的性质,结合等差数列的通项公式,计算可得
条件
易错点
注意等差数列和等比数列的性质的合理运用.
知识点
13.已知
①
②
③若

④若

其中正确结论的序号是 ▲ 
正确答案
② ④
解析
1)使用特例法对选项排除,比如数列
2)使用基本不等式
3)使用等比数列的性质
所以选② ④
考查方向
解题思路
本题的解题思路
1)使用特例法对选项排除,比如数列
2)使用基本不等式
3)使用等比数列的性质
易错点
本题易于错在对等比数列的概念和性质不熟
知识点
2.已知等比数列{an}中,

正确答案
解析




考查方向
解题思路
1)将

2)求
3)将
易错点
本题易在运算上出现错误,也容易按等差数列的性质做题.
知识点
已知等差数列



16.求
17.设等比数列






正确答案
(Ⅰ)
解析
试题分析:(Ⅰ)由已知及等差数列的通项公式和前n项和公式可得关于数列的首项a1和公式d的二元一次方程组,解此方程组可求得首项及公差的值,从而可写出此数列的通项公式.
试题解析: (1)设

化简得
解得
故通项公式

考查方向
解题思路
本题考查等差数列的概念、通项公式及前n项的求和公式,利用方程组思想求解.本题属于基础题.
易错点
等差数列性质的运用
正确答案

解析
试题分析: (Ⅱ)由(Ⅰ)的结果可求出b1和b4的值,进而就可求出等比数列的公比,再由等比数列的前n项和公式



设


故

考查方向
解题思路
本题考查等比数列的概念、通项公式及前n项的求和公式,利用方程组思想求解.本题属于基础题.
易错点
注意运算的准确性
18.
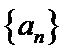
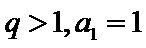
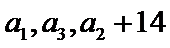
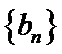
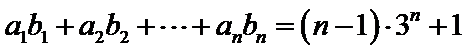
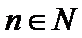
(I)求数列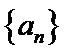
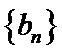
(II)若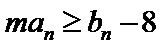
正确答案
见解析
解析
考查方向
解题思路
1)借助等差数列性质求出
2)利用由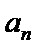
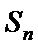
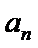
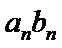
3)对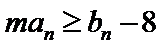
4)讨论新数列单调性,并求出最值
易错点
本题第一问忽略验证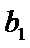
知识点
10. 已知数列




正确答案
解析
由










A选项不正确,B选项不正确,D选项不正确,所以选C选项。
考查方向
解题思路
由等差数列等比数列的性质,把

作差法比较大小。
易错点
等差等比数列性质不熟悉,没有发现第


转化思想,没想到把

知识点
已知等比数列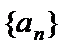
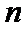
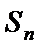
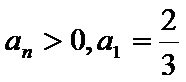
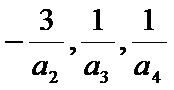
22.求数列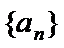
23.设数列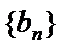
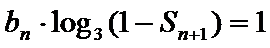
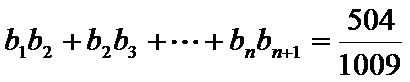
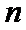
正确答案
(Ⅰ)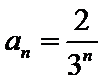
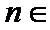

解析
(Ⅰ)设等比数列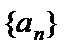
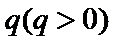
∵ 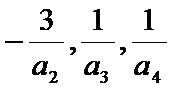
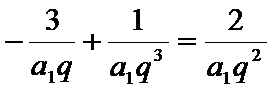
∴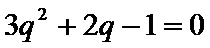
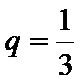
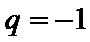
∴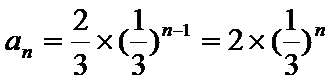
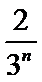
∴数列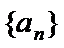
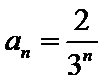
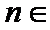

考查方向
解题思路
先根据题中给出的条件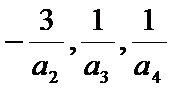
易错点
对于题中给出的条件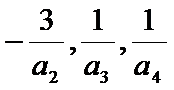
正确答案
(Ⅱ)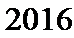
解析
(Ⅱ)由(Ⅰ)知,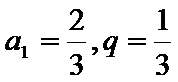
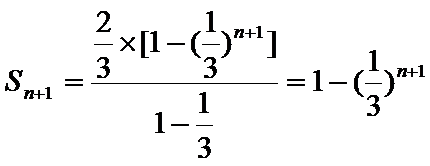
∵数列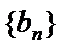
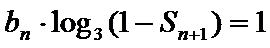
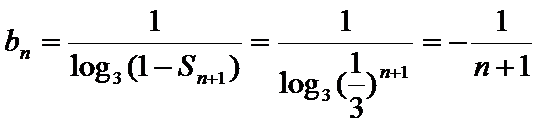
∴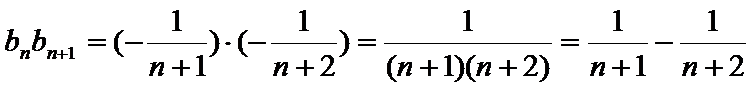
∴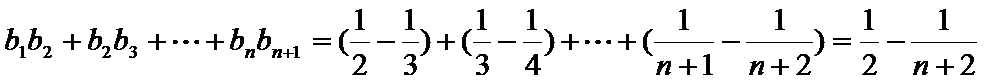
由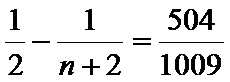
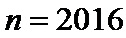
∴满足方程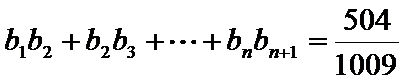
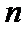
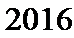
考查方向
解题思路
1.先根据题中给出的条件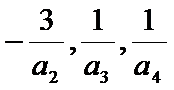
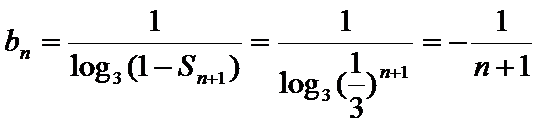
易错点
1.对于题中给出的条件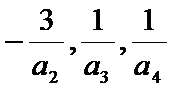
16. 设








正确答案
解析
f(
























考查方向
解题思路
可利用倒序相加求
易错点
求

知识点
11.已知递增的等差数列







正确答案


解析
故此题答案为

考查方向
解题思路
先根据



易错点
本题易在求和项数的判断上出现错误。
知识点
9.已知数列




的前

正确答案
解析
由




考查方向
解题思路
先判断出该数列是一个等差数列,然后再求最值。
易错点
不会转化来做。
知识点
扫码查看完整答案与解析