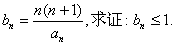数列_章节学习_百度题库

1

题型：填空题

|

填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

1

题型：简答题

|

简答题 · 18 分

设项数均为（）的数列、、前项的和分别为、、.

已知（），且集合

（1）已知，求数列的通项公式；

（2）若，求和的值，并写出两对符合题意的数列、；

（3）对于固定的，求证：符合条件的数列对有偶数对.

正确答案

见解析

解析

（1）时，

时，，不适合该式

故，

（2）

又

得，=46，=26

数列、可以为：

① 16,10,8,12；14,6,2,4 ② 14,6,10,16；12,2,4,8

③ 6,16,14,10；4,12,8,2 ④ 4,14,12,16；2,10,6,8

⑤ 4,12,16,14；2,8,10,6 ⑥ 16,8,12,10；14,4,6,2

（3）令，（）

又=，得

=

所以，数列对（，）与（，）成对出现。

假设数列与相同，则由及，得，，均为奇数，矛盾！

故，符合条件的数列对（，）有偶数对。

知识点

分组转化法求和

1

题型：简答题

|

简答题 · 14 分

数列中，，是前项和，且.

(1)求数列的通项公式；

(2)若，求数列的前项和，并比较与2的大小；

正确答案

见解析。

解析

（1）

知识点

由递推关系式求数列的通项公式分组转化法求和数列与不等式的综合

1

题型：简答题

|

简答题 · 13 分

设数列满足，,且对任意，函数满足

(1)求数列的通项公式；

（2）若，求数列的前项和.

正确答案

见解析

解析

由

所以，

是等差数列。

而

（2）

知识点

导数的运算等差数列的判断与证明等比数列的判断与证明分组转化法求和

1

题型：填空题

|

填空题 · 5 分

数列的前项和为，若数列的各项按如下规则排列：

则若存在正整数，使，则

正确答案

解析

略

知识点

等差数列的基本运算等差数列的前n项和及其最值分组转化法求和

1

题型：简答题

|

简答题 · 12 分

设{an}是公比为正数的等比数列，a1＝2，a3＝a2＋4。

（1）求{an}的通项公式；

（2）设{bn}是首项为1，公差为2的等差数列，求数列{an＋bn}的前n项和Sn。

正确答案

见解析。

解析

知识点

由数列的前几项求通项分组转化法求和等差数列与等比数列的综合

1

题型：简答题

|

简答题 · 5 分

从小到大排列的三个数构成等比数列，它们的积为8，并且这三个数分别加上2、2、1后成等差数列中的.

（1）求数列的通项公式；

（2）若，数列的前项和为，求.

正确答案

见解析。

解析

知识点

分组转化法求和

1

题型：简答题

|

简答题 · 12 分

在数列中，，.

（1）求数列的通项公式；

（2）求证：数列是等差数列；

（3）设数列，求的前项和.

正确答案

见解析。

解析

（1）,∴数列是首项为，公比为的等比数列，

∴.…………………………………………………………………3分

（2） ………………………………………………………………4分

∴.………………………………………………………6分

∴，公差

∴数列是首项，公差的等差数列. ………………………………7分

（3）由（1）知，,

∴ ……………………………………………………8分

∴

……………………………10分

…………………………12分

知识点

由递推关系式求数列的通项公式等差数列的判断与证明分组转化法求和

1

题型：填空题

|

填空题 · 5 分

数列的项是由1或2构成，且首项为1，在第个1和第个1之间有个2，即数列为：1，2，1，2，2，2，1，2，2，2，2，2，1，…，记数列的前项和为，则；，

正确答案

36,3981

解析

略

知识点

分组转化法求和

1

题型：简答题

|

简答题 · 12 分

已知,数列满足,数列满足；数列为公比大于的等比数列，且为方程的两个不相等的实根。

（1）求数列和数列的通项公式；

（2）将数列中的第项，第项，第项，……，第项，……删去后剩余的项按从小到大的顺序排成新数列，求数列的前项和.

正确答案

见解析。

解析

（1），

……………………………………………3分

因为为方程的两个不相等的实数根.

所以，……………………………………………………………4分

解得：，,所以：……………………………………………………6分

（2）由题知将数列中的第3项、第6项、第9项……删去后构成的新数列中的奇数列与偶数列仍成等比数列，首项分别是，公比均是 …………9分

………………………………12分

知识点

等比数列的判断与证明分组转化法求和数列与函数的综合

1

题型：简答题

|

简答题 · 14 分

已知各项均不相等的等差数列的前5项和，又成等比数列。

（1）求数列的通项公式；

（2）设为数列的前项和，问是否存在常数，使，若存在，求的值；若不存在，说明理由。

正确答案

见解析。

解析

（1）设数列的公差为，由已知得，

又成等比数列，所以

解得：

所以

（2）

所以

故存在常数

知识点

分组转化法求和

1

题型：简答题

|

简答题 · 12 分

已知函数，数列{}的前n项和为，点都在函数y＝f（x）的图象上。

（1）求数列{}的通项公式；

（2）令，是数列{}的前n项和，求；

（3）令

正确答案

见解析。

解析

知识点

分组转化法求和

1

题型：简答题

|

简答题 · 12 分

已知等比数列成等差数列。

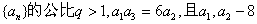
（1）求数列{an}的通项公式；

（2）设

正确答案

见解析。

解析

知识点

分组转化法求和

1

题型：简答题

|

简答题 · 12 分

已知点（1,2）是函数的图象上一点，数列的前n项和.

（1）求数列的通项公式；

（2）将数列前2013项中的第3项，第6项，…，第3k项删去，求数列前2013项中剩余项的和.

正确答案

见解析。

解析

（1）把点（1,2）代入函数，得.……………………（1分）

…………………………………………（2分）

当时，…………………………………（3分）

当时，

……………………………………………（5分）

经验证可知时，也适合上式，

.…………………………………………………………（6分）

（2）由（1）知数列为等比数列，公比为2，故其第3项，第6项，…，第2013项也为等比数列，首项公比为其第671项………………………………………………………………（8分）

∴此数列的和为……………………（10分）

又数列的前2013项和为

…………………………………（11分）

∴所求剩余项的和为…（12分

知识点

由an与Sn的关系求通项an分组转化法求和

1

题型：填空题

|

填空题 · 5 分

对于每一个正整数，设曲线在点（1,1）处的切线与轴的交点的横坐标为，令，则= 。

热门试卷

正确答案

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点