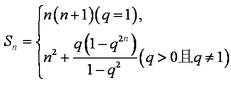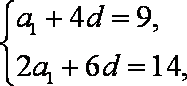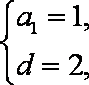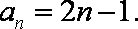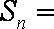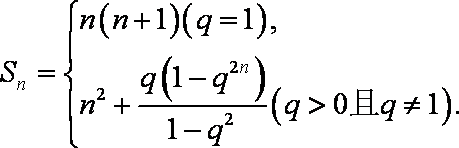- 数列
- 共2062题
已知等差数列

(1)求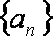
(2)若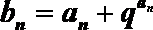
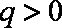
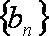
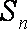
正确答案
(1)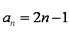
解析
解析:(1)设
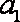
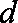
由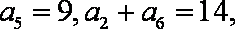
解得
所以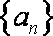
(2)由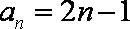
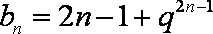
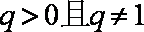
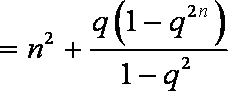
② 当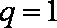
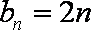
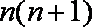
所以数列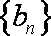
知识点
在等差数列


(1)求数列
(2)设


正确答案
见解析
解析
解析:本题主要考查等差数列、等比数列、数列求和等基础知识;考查推理论证与运算求解能力。
(1)设等差数列

则
解得
∴
(2)
∵
∴

又

知识点
设公比大于零的等比数列










(1)求数列

(2)设


正确答案
见解析
解析
(1)由


又

则得
所以

(2)


则

即

当



知识点
已知数列



(1)求数列
(2)设





正确答案
见解析
解析
(1)由已知,


即



∴数列

∴
(2)∵


∴
∴
∴
(ⅰ)当

当且仅当

∴
(ⅱ)当

当且仅当


∴
即


综上所述,存在


知识点
等差数列




(1)求数列
(2)设

正确答案
(1)an=n(2)
解析
(1)由

又



(2)根据(1)得

由于函数


而


所以当


即数列

知识点
已知公差不为零的等差数列




(1)求数列
(2)设





正确答案
见解析
解析
解:(1)设公差为

解得:


(2)由题意



知识点
已知数列

(1)求数列
(2)求证:
正确答案
见解析
解析
(1)设等差数列的公差为d,
由

所以

(2)证明:
所以
知识点
设数列{an}的前n项和为Sn,a1=2.且1, 
(1)求数列{an}的通项公式
(2)求数列{nan}的前n项和Tn
正确答案
见解析
解析
(1)证明:∵
∴
∴
∴
又

∴
(2)解:∵
∴

①-②得:
∴
知识点
已知公比不为1的等比数列





正确答案
7
解析


知识点
巳知等比数列{an}的首项和公比都为2,且a1,a2分别为等差数列{bn}中的第一、第三项。
(1)求数列{an}、{bn}的通项公式;
(2)设Cn=
正确答案
见解析。
解析
(1)∵等比数列{an}的首项和公比都为2,
∴
∵a1,a2分别为等差数列{bn}中的第一、第三项
∴b1=2,b3=4
∴bn=n+1;
(2)设Cn=

∴Sn=


知识点
已知数列




(1)求数列

(2)设





正确答案
见解析
解析
解: (1)


由①

当



所以,数列



(2)由(1)

所以
所以

知识点
已知数列{an}是等差数列,{bn}是等比数列,且a1=11,b1=1,a2+b2=11,a3+b3=11。
(1)求数列{an}和{bn}的通项公式;
(2)求数列{|an﹣bn|}的前12项的和S12。
正确答案
见解析
解析
(1)设



则由

可求得:

从而

(2)


知识点
在等差数列







(1)求数列

(2)设



正确答案
见解析
解析
(1)设等差数列



由题意,得

∴

(2)
∴

知识点
已知数列{an}的首项a1=2,前n项和为Sn,且a2,Sn,2an+1成等差。
(1)求数列{an}的通项公式;
(2)记
正确答案
见解析
解析
解:(1)∵

两式相减得

又当n=1时,

∴{an}是首项a1=2,公比为2的等比数列,∴an=2n.
(2)∵
∴
∵

知识点
已知数列





(1)求数列
(2)设



正确答案
见解析
解析
解(1)令


若
若




(2)

由





知识点
扫码查看完整答案与解析