- 数列
- 共2062题
已知曲线





(1)求数列
(2)设梯形



正确答案
(1)
(2)
解析
(1)由
∵

故

(2)∵
∴
∴四边形
,
故
知识点
已知数列{



正确答案
解析
由





知识点
19.已知数列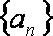
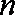
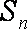
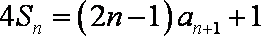
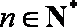
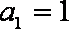
(1)求证:数列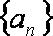
(2)设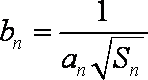
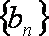
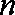
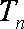
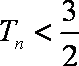
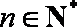
正确答案
见解析。
解析
(1)由题设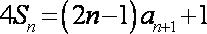
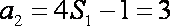
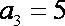
当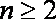
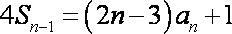
两式相减得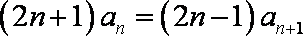
方法一:由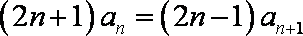
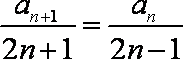

则数列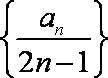
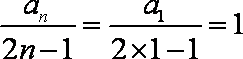
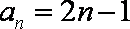
所以数列
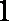
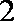
方法二:由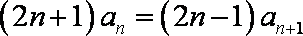
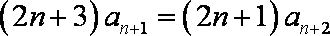
两式相减得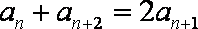
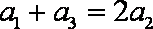
所以数列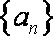
(2)由(Ⅰ)得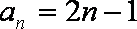
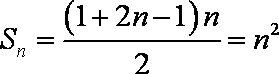
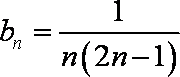
当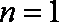
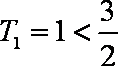
当
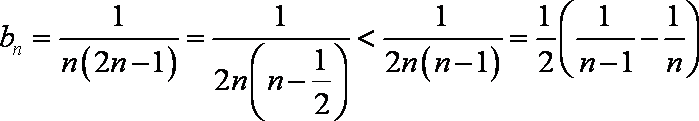
所以
综上所述,命题得证。
知识点
7.某产品在某零售摊位的零售价x(单位:元)与每天的销售量y(单位:个)的统计资料如下表所示:由上表可得回归直线方程

正确答案
解析
由题意知

知识点
11.已知数列



正确答案
26
解析
略。
知识点
14.已知曲线C1与C2的极坐标方程分别为 


正确答案
解析
略。
知识点
已知


(1)求数列
(2)若数列


求数列


正确答案
见解析。
解析
(1)设等差数列

由

由

易得

备注:也可以由


(2)令





而

于是
=

知识点
22.已知a,b为常数,且a≠0,函数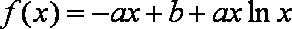
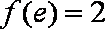
(1)求实数b的值;
(2)求函数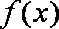
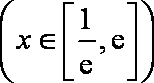
(3)当a=1时,是否同时存在实数m和M(m<M),使得对每一个t∈[m,M],直线y=t与曲线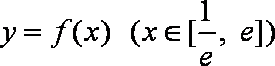
正确答案
见解析。
解析
(1)由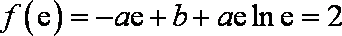
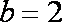
(2)由(Ⅰ),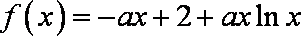

从而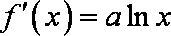
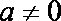
(1) 当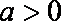
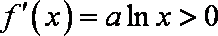
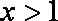
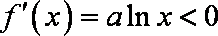
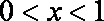
(2) 当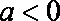
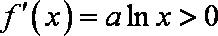
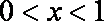
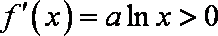
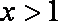
因而, 当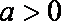
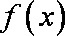
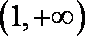
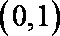
当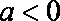
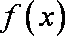
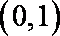
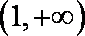
(3)当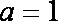
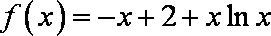
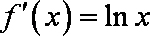
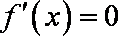
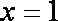
当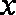


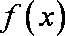
因为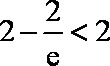
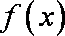

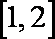
由此可得,
若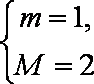

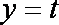
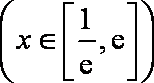
并且对每一个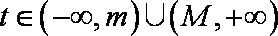
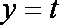
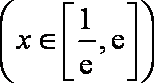
综合以上,当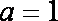
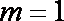

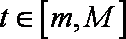
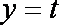
知识点
13.已知数列{an}满足an=,则数列的前n项和为________。
正确答案
解析
所求的前n项和为,
知识点
14.已知{an}是等比数列,
正确答案
解析
由 

数列{anan+1}仍是等比数列:其首项是a1a2=8,公比为
所以,
故答案为
【点评】: 本题主要考查等比数列通项的性质和求和公式的应用.应善于从题设条件中发现规律,充分挖掘有效信息.
知识点
16. 在数列{an}中,a1=

(1)求an,Sn;
(2)设bn=log2(2Sn+1)﹣2,数列{cn}满足cn•bn+3•bn+4=1+n(n+1)(n+2)•2bn,数列{cn}的前n项和为Tn,求使4Tn>2n+1﹣
正确答案
见解析。
解析
(1)由Sn=an+1﹣

两式作差得:an=an+1﹣an,即2an=an+1(n≥2),
∴
又
∴
∴数列{an}是首项为
则

(2)bn=log2(2Sn+1)﹣2=
∴cn•bn+3•bn+4=1+n(n+1)(n+2)•2bn,
即


=


由4Tn>2n+1﹣

即
∴使4Tn>2n+1﹣
知识点
17.数列{an}中,a1=

(1)求数列{an}的通项公式an以及前n项和Sn;
(2)若S1,t(S1+S2),3(S2+S3)成等差数列,求实数t的值。
正确答案
见解析。
解析
(1)由Sn+1﹣Sn=(

又

从而
(2)由(Ⅰ)可得


从而由S1,t(S1+S2),3(S2+S3)成等差数列可得:
知识点
12.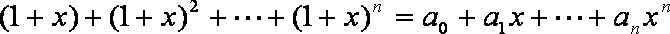
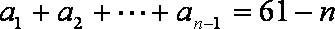
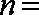
正确答案
5
解析
显然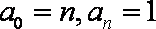
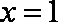
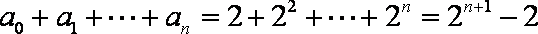
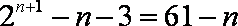
知识点
22.已知数列



(1)求数列


(2)数列





(3)设


正确答案
(1)
(2)
(3)3
解析
(1) 



∴令

∴数列


∴
(2) 由



故
当

于是,
当

当
又

综上,有
(3)

∴

∴数列



知识点
9.若

正确答案
解析

知识点
扫码查看完整答案与解析