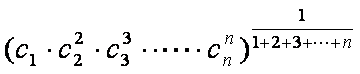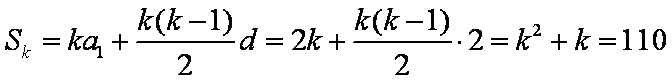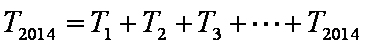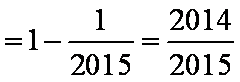- 数列
- 共2062题
11. 已知数列



正确答案
26
解析
解析已在路上飞奔,马上就到!
知识点
19.已知数列





(1)求证:数列
(2) 设





正确答案
见解析。
解析
(Ⅰ) 由题设


当

两式相减得
方法一:由


则数列


所以数列


方法二:由

两式相减得

所以数列
(Ⅱ) 由(Ⅰ)得


当

当

所以
综上所述,命题得证. ………………………………14分
知识点
19.数列{an}中,已知a1=1,n≥2时,an=
(1)求证:数列{bn}是等差数列;
(2)求数列{an}的前n项和Sn。
正确答案
见解析。
解析
(1)证明:由
得:
∴
即bn=bn﹣1+2⇒bn﹣bn﹣1=2(n≥2)
又
∴数列{bn}是首项为2,公差为2的等差数列。
(2)解:由(1)知,bn=2+(n﹣1)×2=2n,
∴
记
则
两式相减得:
=
∴
因此,
知识点
15.已知数列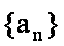
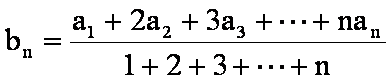
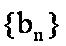
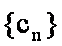
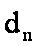
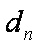
正确答案
解析
由等差数列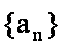
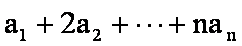
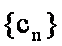
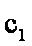
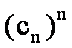
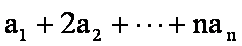
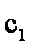
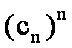

知识点
18.设等差数列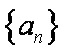
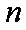
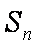
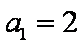
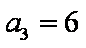
(1)求数列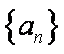
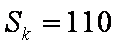
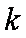
(3)设数列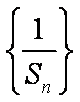
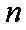
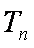
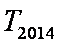
正确答案
见解析。
解析
(1)设等差数列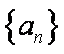
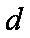
∵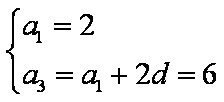
∴
数列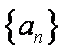
(2)方法一:∵
解得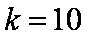
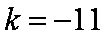
方法二:∵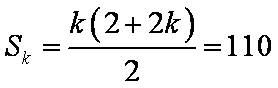
解得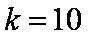
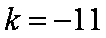
(3)∵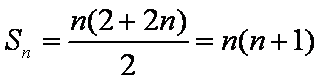

∴
知识点
19.已知数列




(1)求

(2)若数列

(3)求数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.若等差数列





正确答案
17
解析
解析已在路上飞奔,马上就到!
知识点
13.在等比数列



正确答案
22
解析
解析已在路上飞奔,马上就到!
知识点
20.已知曲线









(1)求数列
(2)记





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.如果等差数列


正确答案
解析


知识点
6. 在等比数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知


(1)求
(2)若等比数列




正确答案
(1)
(2)
解析
解析已在路上飞奔,马上就到!
知识点
15.设数列



(1)求


(2)已知





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析