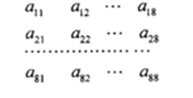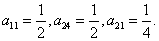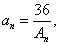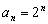- 数列
- 共2062题
观察下列各式:






正确答案
解析
略
知识点
已知等差数列





(1)求数列
(2)求数列

正确答案
(1)
(2)
解析
(1)因为
所以
因为
所以
由①,②及

所以
(2)由

所以 
所以

所以 数列


知识点
已知每项均是正整数的数列




(1)设数列
①求

(2)若

正确答案
见解析
解析
(1)因为数列
所以
所以

(2)一方面,
根据

故

当且仅当
因为


所以
即当



知识点
环保刻不容缓,或许人类最后一滴水将是自己的泪水.某地水资源极为紧张,且受工业污染严重,预计







(1)求
(2)若每年拆除


正确答案
见解析。
解析
(1)设第


当

所以, 当
当
故
(2)









所以,




故当



知识点
一个三角形数表按如下方式构成(如图:其中项数




(1)求第2行和第3行的通项公式

(2)证明:数表中除最后2行以外每一行的数都依次成等差数列;
(3)求


正确答案
见解析
解析
(1)

(2)由已知,第一行是等差数列,
假设第


知第

综上可得,数表中除最后2行以外每一行都成等差数列。---------------------------(9分)
(3)由于

所以
由

于是

又因为




知识点
对于三次函数










正确答案
解析
略
知识点
已知m是两个正数2和8的等比中项,则圆锥曲线

正确答案
解析
略
知识点
已知等差数列


(1)求数列
(2)若数列





正确答案
见解析。
解析
(1)设数列

解得:

(2) 




知识点
64个正数排成8行8列,如右图所示:
其中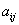
(1)求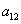
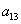
(2)记第n行各项之和为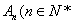
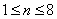
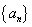
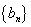
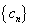
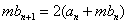
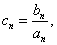
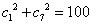
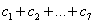
(3)对(2)中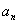
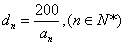
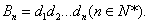
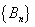
正确答案
见解析。
解析
(1)因为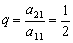
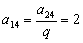
又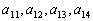
所以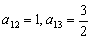
(2)由(1)得,第一行所成等差数列公差为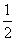
所以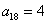
因为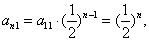
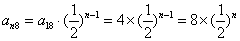
所以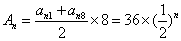
所以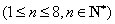
因为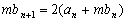
所以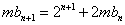
整理得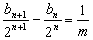
而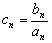
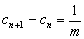
所以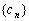
故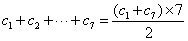
因为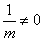
所以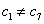
所以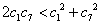
所以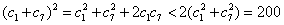
所以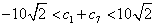
所以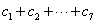
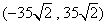
(3)因为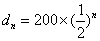
所以当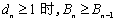
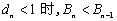
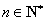
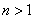
所以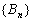
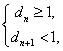
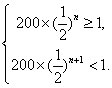
解得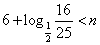
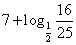
又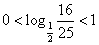
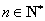
所以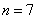
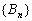
知识点
若①


正确答案
25
解析
略
知识点
定义:对于各项均为整数的数列











(1)

(2)




给出下面三个数列:
①数列


②数列
③数列
具有“

正确答案
①、②
解析
略
知识点
已知数列


(1)若

(2)若

① 记

② 若数列

正确答案
见解析
解析
(1)当

又


(2)①因为对任意的


所以,数列
②设


所以,
即数列
设
(其中

当


当

(Ⅰ)若



(Ⅱ)若



综上所述,集合
当

当



知识点
若数列


正确答案
解析
略
知识点
已知数列




正确答案
6或7
解析
略
知识点
若矩阵

正确答案
解析
略
知识点
扫码查看完整答案与解析