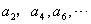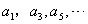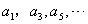- 数列
- 共2062题
19.巳知各项均为正数的等差数列






(I)求数列

(II)设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知等差数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如果数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知等差数列







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.设




(1)求数列
(2)若数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.数列




(Ⅰ)求数列
(Ⅱ)设



正确答案
解:(Ⅰ)由已知:对于

∴
①-②得
∴
∵

∴数列
又n=1时,

∴

(Ⅱ) 解:由(1)可知
解析
解析已在路上飞奔,马上就到!
知识点
18. 在数列

(1)设

(2)求数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.将参加夏令营的600名学生编号为:001,002,……600,采用系统抽样方法抽取一个容量为50的样本,且随机抽得的号码为003.这600名学生分住在三个营区,从001到300在第Ⅰ营区,从301到495住在第Ⅱ营区,从496到600在第Ⅲ营区,三个营区被抽中的人数依次为 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.已知数列







(1)求数列
(2)设




正确答案
(2)∵


∴
∴
∴
(ⅰ)当

当且仅当

∴
(ⅱ)当

当且仅当


∴
即


综上所述,存在


解析
解析已在路上飞奔,马上就到!
知识点
20.已知数列



(1)求数列
(2)若函数

(3)设






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.无穷数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.在数列



① 在差等比数列中
② 等差数列一定是差等比数列
③ 等比数列一定是差等比数列
④差等比数列中可以有无数项为
其中正确的判断是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.等比数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.设等差数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析