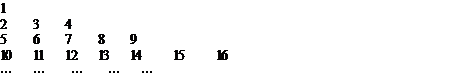- 数列
- 共2062题
4. 等差数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知等比数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.将正整数排成下表,则数表中的2008出现在第_______行。
正确答案
45
解析
解析已在路上飞奔,马上就到!
知识点
20.已知数列








(1)求数列



(2)若对任意的


(3)是否存在正整数


正确答案
(2)①当

即需不等式




②当

即需不等式








综合①、②可得

(3)
若

即
由

即

又



因此,当且仅当



[另解] 因为



解析
解析已在路上飞奔,马上就到!
知识点
5. 设等差数列





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 已知等差数列




(Ⅰ)求

(Ⅱ)若



正确答案
解:(Ⅰ)设等差数列



所以有


(Ⅱ)∵
∴当


以上

即
当



解析
解析已在路上飞奔,马上就到!
知识点
5.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.正项等比数列{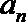
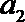

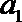
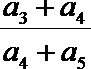
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知数列




(1)求
(2)求数列
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知等差数列

正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
8.已知等比数列




正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
11.将正奇数下表其中第





正确答案
60
解析
解析已在路上飞奔,马上就到!
知识点
13.数列





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知数列



(1)求数列
(2)若函数

(3)设






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析