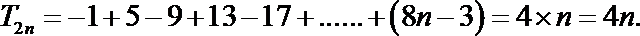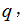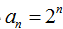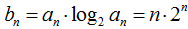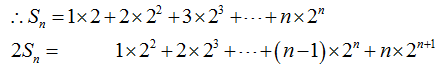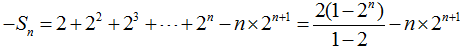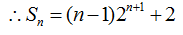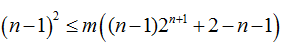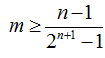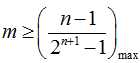- 数列
- 共2062题
20.已知数列


(1)若

(2)若

①记

②若数列

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.设函数f(x)的定义域为R,当x<0时,0<f (x)<1,且对任意的实数x, y∈R,有f(x+y)=f (x)f (y);
(1)求f (0), 并证明:当x∈R时, f (x)>0;
(2)判断并证明函数f (x)在R上的单调性;
(3)设数列{an}各项都是正数,且满足a1=f (0), f(an+12-an2)=


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.观察下列各式的规律,猜测第n个等式为_________
1=1;
1-4=-3;
1-4+9=6;
1-4+9-16=-10;
……
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知a=ln





正确答案
解析
令f(x)=ln x-x,则f'(x)=

当0<x<1时,f'(x)>0,即函数f(x)在(0,1)上是增函数.
∵
∴a>b>c.故选A.
知识点
8.已知数列{bn}中,bn+1=

正确答案
4与0
解析
bn+1=



由b1=0,得


当n为奇数时,
当n为偶数时,
综上可知,数列{bn}的最大项为b2=4,最小项为b1=0.
知识点
9.设F是椭圆
正确答案
解析
若公差d>0,则|FP1|最小,|FP1|=
数列中的最大项为
则



注意到d>0,得0<d≤
若d<0,易得-
那么d的取值范围为
知识点
4.已知数列满足a1=1,an-1=2an+1(n≥2,n∈N*),则数列的前6项和为( )
正确答案
解析
因为an-1=2an+1(n≥2,n∈N*),所以

所以是首项为2,公比为
所以(a1+1)+(a2+1)+…+(a6+1)= 
所以a1+a2+…+a6=

知识点
17.已知等差数列{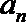
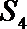
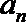
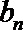
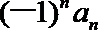
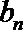
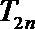
正确答案
an=4n-3; T2n=4n
解析
⑴由已知条件: 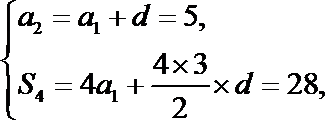
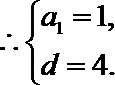
⑵由⑴可得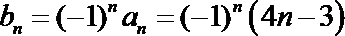
考查方向
本题主要考查数列的综合运算
易错点
本题易在求和时发生错误。
知识点
12.



且

正确答案
8
解析


所以

所以

所以填8
考查方向
解题思路
先求出a7的值,然后再求答案
易错点
不转换建立关系,直接算
知识点
3.在数列


正确答案
解析
由已知,
所以
所以
应选A
考查方向
本题主要考查数列与等比数列的概念,
考查运算能力和推理能力,难度不大。
解题思路
判断数列
由等比数列通项公式的一般式,求得结果。
应选A
易错点
想不到用等比数列通项公式的一般式解决;
用一般方法时,公比易算错。
知识点
4.已知一组数据4.7,4.8,5.1,5.4,5.5,则该组数据的方差是_______________.
正确答案
0.1
知识点
19. 已知单调递增的等比数列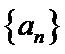
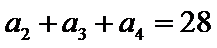
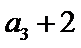
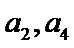
(I)求数列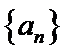
(II)设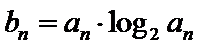
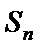
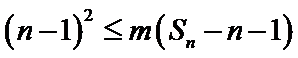
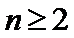
正确答案
(1)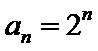
(2)
解析
试题分析:本题属于数列应用中的基本问题,题目的难度是逐渐由易到难,直接按照步骤来求
(Ⅰ)设等比数列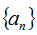
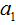
由题意可知: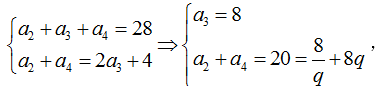
∴
所以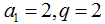
(Ⅱ)令
相减得
若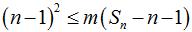
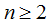
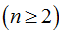
令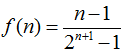
考查方向
解题思路
本题考查数列的性质,解题步骤如下:
1、利用基本量法求出通项;
2、利用错位相减法求和,恒成立问题转为最值问题
易错点
第一问中的辅助角容易计算错误
知识点
17.已知等差数列



(Ⅰ)求
(Ⅱ)若



正确答案
(Ⅰ)
(Ⅱ)
解析
试题分析:本题属于数列的基本运算题,难度不大,只需要用公式直接求出结果即可。(Ⅰ)设等差数列

解得
所以

(Ⅱ)由(Ⅰ)知,

当

当

综上,

考查方向
解题思路
本题主要考查等差数列的定义、通项公式、前n项和公式,解题步骤如下:由公式列出方程组,解出即可;分n为奇数和偶数分别求出结果。
易错点
1第一问列出方程组以后,求解易出错;
2.第二问不能对n正确进行分类。
知识点
15. 等差数列




(Ⅰ)求
(Ⅱ)求满足不等式

正确答案
(Ⅰ)
(Ⅱ)
解析
(Ⅰ)设数列

因为

因为


所以
(Ⅱ)因为


所以

解得


考查方向
本题考查了等差数列的通项公式、前n项和公式.在近几年的各省高考题出现的频率非常高.
解题思路
(Ⅰ)将通项公式代入
(Ⅱ)代入求和公式,解不等式即可.
易错点
移项时注意变号.
知识点
17.设数列




(1)求数列

(2)设



正确答案
(1)

(2)
解析
(1)



(2)
两式相减得
考查方向
本题主要考查了数列的通项公式和求和
解题思路
(1)利用
(2)利用错位相减法求出前n项和本题考查导数的性质,
易错点
(1)利用定义求通项公式
(2)第二问中错位相减法计算的准确性;
知识点
扫码查看完整答案与解析