- 数列
- 共2062题
19.已知正项数列



(1)求数列
(2)若



正确答案
(1)由题意知

当
当


整理得
所以数列
(2)

两式相减得
所以
所以
解析
解析已在路上飞奔,马上就到!
知识点
21.设数列






(Ⅰ) 求数列
(Ⅱ)是否存在实数


正确答案
(Ⅰ)由题意可得:



①─②得



(Ⅱ)解法一:
若
则
得
又


故存在实数

解法二:
欲使


故存在实数

解析
解析已在路上飞奔,马上就到!
知识点
21.已知各项均为正数的数列


(1)求数列
(2)若



正确答案
(1)由已知 
当

①-② 得
整理得
又n=1时 


故
(2)由
得
则
=
=

①-②,得
=
解得
解析
解析已在路上飞奔,马上就到!
知识点
23.已知数列




(1)能否唯一确定数列

(2)能否求得
(3)若





正确答案
(1)
即
由于

因此不能唯一确定数列
(2)为使
为使

∴ 


(3)

∴ 

∴
解析
解析已在路上飞奔,马上就到!
知识点
20. 设数列{an}的前n项和为Sn,对任意的正整数n,都有an =5Sn+1成立,记
(I)求数列{an}与数列{bn}的通项公式;
(Ⅱ)设数列{ bn }的前n项和为Rn,是否存存正整数k,使得Rn≥4k成立?若存在,找出一个正整数k;若不存在,请说明理由;
(III)记


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
24.已知数列


(1)求该数列的通项公式;
(2)令


正确答案
解:(1)



作差得:

又
知





(2)由(1)得: 




解析
解析已在路上飞奔,马上就到!
知识点
19.已知数列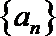
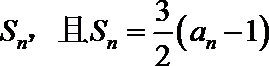
(I)求数列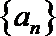
(II)设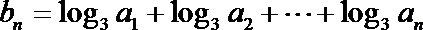
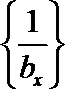
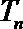
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知数列{an}中,a1=2,前n项和为Sn,对于任意n≥2,3Sn-4,an,
(I)求数列
(II)若数列



正确答案
(I)∵n≥2时,3Sn-4,an,2-
∴
即 
∴ 
两式相减,得

∴a2,a3,…an,…成等比数列.
∵a1=2 当n =2时,a2= 
∴a1,a2,a3,…an,…成等比数列,
∴an=2
(II)由(I)得 
∴

∵ 
∴ 
解析
解析已在路上飞奔,马上就到!
知识点
15.已知定义在R上的函数









正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
21.数列
(1)求证:数列
(2)求数列
(3)等差数列


正确答案
(1)
又
所以
数列
(2)
(3)
等差数列
设公差为
则
又

解析
解析已在路上飞奔,马上就到!
知识点
19.设数列
(I)求数列
(II)是否存在正整数n使得

正确答案
解:(I)




(II)

解析
解析已在路上飞奔,马上就到!
知识点
3.已知数列{an}的前n项和为Sn,且an=Sn·Sn-1 (n≥2),a1=- 
正确答案
解析
由an=Sn·Sn-1 (n≥2),得

又

∴
∴a12=S12-S11=- 


知识点
19.已知数列


(1)证明:数列

(2)设

正确答案
解:(1)
(2)
解析
解析已在路上飞奔,马上就到!
知识点
13.Sn为等比数列{an}的前n项和,满足Sn=2an-1,则{an}的公比q= 。
正确答案
2
解析
当






考查方向
解题思路
1.先令

2. 令

3.求出
易错点
不清楚前n项和

知识点
16.已知数列




正确答案
解析








考查方向
解题思路
详见解析
易错点
不能够想到

知识点
扫码查看完整答案与解析


























































































