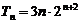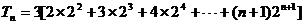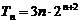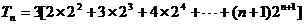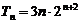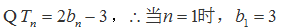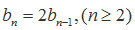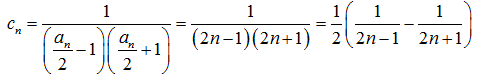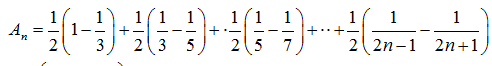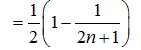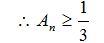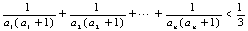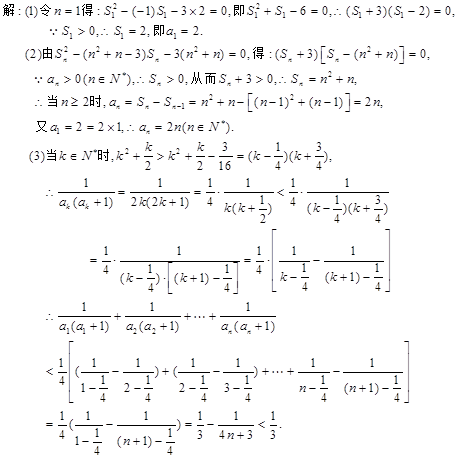- 数列
- 共2062题
19. 已知数列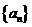
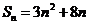
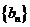
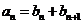
(I)求数列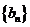
(II)令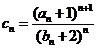
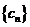
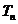
正确答案
(Ⅰ)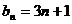
解析
试题分析:(Ⅰ)由题意得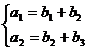
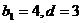
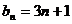
(Ⅱ)由(Ⅰ)知
利用“错位相减法”即得
试题解析:(Ⅰ)由题意当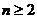
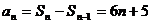
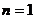
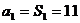
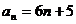
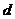
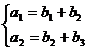
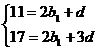

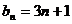
(Ⅱ)由(Ⅰ)知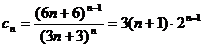
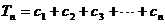
,所以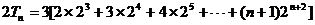
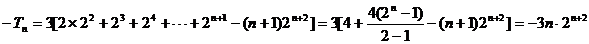
所以
考查方向
知识点
4.已知





正确答案
解析
考查方向
解题思路
本题属于常规题,使用直接法,计算找出规律,分组求和,
易错点
该题易错于无法找到数列的规律性
知识点
15.已知数列




正确答案
解析



考查方向
解题思路
本题考查转化思想的能力,解题步骤如下:将


易错点
不会转化成关于和有关的式子。
知识点
18. 已知正项数列







正确答案
见解析
解析
试题分析:本题属于数列中的基本问题,题目的难度是逐渐由易到难.
(1)由题意知:①当n=1时,∵2S1=
∴
②当n≥2时,
∴
∴
∴ 数列
∴
(2)由(1)知
∴
∴
相减得

∴ 
考查方向
解题思路
本题考查数列问题,解题步骤如下:1、利用an与Sn的关系求解。2、利用等比数列的求和公式求解。
易错点
等比数列分项时项数易错。
知识点
19. 设数列




(I)求数列

(II)将数列






正确答案
(1)
解析
试题分析:本题属于数列中的基本问题,题目的难度是逐渐由易到难.
(1)由已知得
(2)由已知得:

首项分别是

T2006=(c1+c3+……+c2015)+(c2+……+c2016)=
考查方向
解题思路
本题考查数列问题,解题步骤如下:
1、利用an与Sn的关系求解。
2、利用等比数列的求和公式求解。
易错点
等比数列分项时项数易错。
知识点
7. 数列{an}的通项公式an=ncos,其前n项和为Sn,则S2016等于( )
正确答案
解析
其中所有的奇数项都为0,而偶数项是分别为第二项是-2,第四项是4,第六项是-6,第八项是8,这样可以将每2项相加放在一起,刚好有1008个偶数项,即可以组成504组,每组的值为2,所有答案就为1008,故A正确。
考查方向
解题思路
算出前4项并找到这个数列的规律,最后用求和公式解决。
易错点
1、不能找到数列的周期性,没有找到规律导致无法计算下去。
知识点
13.若数列


正确答案
28
解析
由于
考查方向
解题思路
将连续两项看成是一项,就可以构造出一个等差数列。
易错点
公差是4的数列。
知识点
18. 已知数列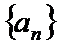
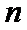
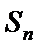
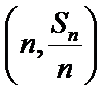
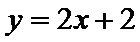
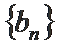
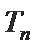
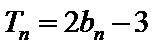
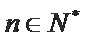
(Ⅰ)求数列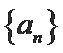
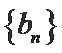
(Ⅱ)设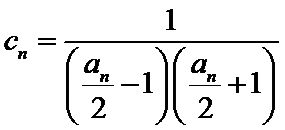
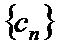
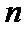
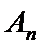
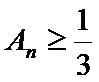
正确答案
(1)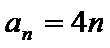
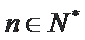
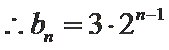
解析
试题分析:本题属于数列中的基本问题,题目的难度是逐渐由易到难.
解:(Ⅰ)由题意,得 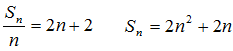
当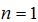
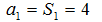
当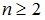
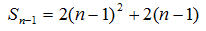
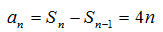
综上,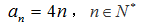
又
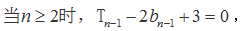
数列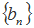
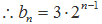
(Ⅱ)
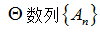
考查方向
解题思路
本题考查数列问题,解题步骤如下:
1、利用an与Sn的关系求解。
2、利用等比数列的求和公式求解。
易错点
等比数列分项时项数易错。
知识点
18. 设数列

(1)求数列

(2)是否存在正整数n,使得
正确答案
(1)
(2)
解析
本题属于三角函数的图像与性质及正余弦定理的综合应用问题,属于简单题,只要掌握相关函数的知识,即可解决本题,解析如下:
解:(1)
所以
两式相减得:
即

所以

所以
所以
所以
所以
所以

考查方向
本题考查了数列的相关知识点,属于简单题。
易错点
相关知识点不熟悉导致出错。
知识点
19. 设数列






(1)求证:数列

(2)令








正确答案
见解析
解析
解:(1)当


代入

而
∴数列
∴


又
(2)当



∴
故
当

若
则等式


若


∵



∴当且仅当


综上可知,当


当


考查方向
解题思路
利用

易错点
忽略n的范围的讨论。
知识点
设数列{an}(n=1,2,3…)的前n项和Sn满足Sn=2an-a3,且a1,a2+1,a3成等差数列.
16.求数列的通项公式;
17.设数列
正确答案
an=2n;
解析
由已知Sn=2an-a1,有
an=Sn-Sn-1=2an-2an-1(n≥2)
即an=2an-1(n≥2)
从而a2=2a1,a3=2a2=4a1,
又因为a1,a2+1,a3成等差数列
即a1+a3=2(a2+1)
所以a1+4a1=2(2a1+1),解得a1=2
所以,数列{an}是首项为2,公比为2的等比数列
故an=2n.
考查方向
解题思路
1.第(1)问先根据题中给出的条件得到an=2an-1(n≥2),然后再求出a1=2,即可求出an=2n.
易错点
1.不会根据Sn=2an-a3求出an=2an-1(n≥2);
正确答案
Tn=
解析
由上题得
所以Tn=
考查方向
解题思路
第(2)问根据第(1)问的结论直接求解即可。
易错点
.求前n项和时对于项数出错。
3. 设




正确答案
考查方向
本题主要考查了数列的定义、等比数列的基本量运算与公式,在近几年的各省高考题出现的频率较高,常单独命题或与等差数列给合,考查基本公式、运算和性质。
解题思路
由方程思想列出关于公差与首项的等量关系,进而求解。
易错点
审题错误(等差看成等比),或者由运算导致出错
知识点
刘某诉某医院医疗纠纷案件,法院判决医院赔偿刘某损失5000元,医院拒不执行,法院在强制执行的过程中扣押了医院的一台叮机。某医疗设备公司提出该设备是医院借用的,所有权属于医疗设备公司。则法院的处理措施错误的是( )。
A.法院审查医疗设备公司的主张理由是否成立
B.人民法院在审查期间可以对财产采取查封、扣押等措施
C.人民法院在审查期间对该机器进行拍卖
D.人民法院在审查后认为医疗设备公司的主张成立的,应当由院长批准中止执行
正确答案
C
解析
[考点] 案外人执行异议 [解析] 本题考查的是案外人执行异议。案外人执行异议是指案外人对执行的标的提出了不同的意见并主张部分或者全部的权利,这种异议牵扯到对案外人利益的保护,法院必须认真处理。本案中,医疗设备公司针对CT机主张的所有权就属于这种异议。《民事诉讼法》第208条规定:执行过程中,案外人对执行标的提出异议的,执行员应当按照法定程序进行审查。理由不成立的,予以驳回,理由成立的,由院长批准中止执行。如果发现判决、裁定确有错误,按照审判监督程序处理。据此,A、D选项都是正确的。《最高人民法院关于执行工作若干问题的规定(试行)》(简称《执行规定》)第7l条规定:对案外人提出的异议,执行法院应当依照《民事诉讼法》第208条的规定进行审查。审查期间可以对财产采取查封、扣押、冻结等保全措施,但不得进行处分。正在实施的处分措施应当停止。经审查认为案外人的异议理由不成立的,裁定驳回其异议,继续执行。据此,在审查期间可以采取查封、扣押措施,但是不能进行处分,拍卖应是不允许的。故B项正确,C项不正确。
设各项为正数的数列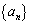
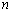

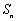
(1)求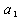
(2)求数列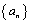
(3)证明:对一切正整数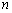
正确答案
见解析。
解析
知识点
已知等差数列









23.求数列

24.记

正确答案
解析
(1)由





从而

在已知
当





考查方向
解题思路
先解一元二次方程可得


易错点
熟悉已知递推关系求数列通项公式的方法
正确答案


考查方向
解题思路
求出数列
易错点
熟悉求差比较法
扫码查看完整答案与解析