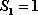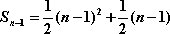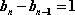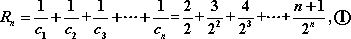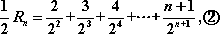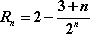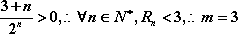- 数列
- 共2062题
对于数列






(1) 若

(2) 在






(3) 他在研究过程中猜想了一个命题:“对于首项为正整数









正确答案
见解析
解析
解析:(1)由a32=a1a5,
即(a1+2d)2=a1(a1+4d),得d=0.
(2) 解:an=1+3(n-1),如bn=4n-1便为符合条件的一个子数列. …
因为bn=4n-1=(1+3)n-1=1+


这里M=


所以,bn=1+3M =1+3 [(M+1)-1]是{an}中的第M+1项,得证. ……………….11分
(注:bn的通项公式不唯一)
(3) 该命题为假命题.
由已知可得
因此,

故 



又



所以,

知识点
如果存在常数







(1)若数列:



(2)若有穷递增数列



(3)已知有穷等差数列





正确答案
见解析
解析
(1)因为数列:

所以

故
即
(

因为有穷数列

所以
又因为数列

则
故
(3)数列
设数列




若
即对数列

同理可得:若

由“兑换数列”的定义可知,数列
又因为数列



知识点
已知数列










(1)求


(2)是否存在实数



正确答案
见解析
解析
(1)








……………………………. 6分
(2)
…………………………. 8分




因此
知识点
已知


(1)证明:数列
(2)设数列




(3)已知






正确答案
见解析。
解析
(1)证明:由已知
∵
∴
(2)由(1)得
∵
∴
(3)∵
(另法:

∴
显然
又
知识点
设








(1)求

(2)求证:
(3)是否存在正整数



正确答案
见解析
解析
解析:(1)设数列





∴

∵



(2)
∴
∴
(3)由(2)知,



∴ 
即
当





当





当





……………15分
当



所以,此时不存在正整数m,n,且1<m<n,使得
综上,存在正整数m=2,n=16,且1<m<n,使得
另解:
(3)由(2)知,

∵

取倒数再化简
当



而
所以,此时不存在正整数m、n , 且1<m<n,使得
综上,存在正整数m=2,n=16,且1<m<n,使得
知识点
已知等差数列







(1)求数列
(2)设数列



正确答案
见解析
解析
(1)解:因为数列
所以

依题意,有
解得

所以数列


(2)证明:由(1)可得
所以
所以

因为
因为

所以
所以
知识点
已知数列
(1)求证数列
(2)求数列


(3)设数列





正确答案
见解析
解析
(1)

……………2分



公比为2,
(2)
当

当

因此,
(3)


因此不等式为 3(1-k2
















知识点
定义数列






(1)求数列


(2)问是否存在正整数


正确答案
见解析。
解析
(1)对任意正整数


所以数列





对任意正整数


所以数列
或
对任意正整数

所以数列


或
(2)

从而

①当


②当


③当


使得
从而




综上可知,符合条件的正整数对

知识点
已知函数

(1)当

(2)设






(3)利用函数







在上述构造过程中,若




正确答案
见解析
解析
(1)当

图像如图(2分)
基本性质:(每个2分)
奇偶性:既非奇函数又非偶函数;
单调性:在

零点:
最值:无最大、小值,(6分)
(2)
当



当



因此,数列中的最大项为
最小项为
(3)根据题意,只需当

亦即方程

将


由


即实数

知识点
已知






(1)若



(2)若对于


正确答案
见解析
解析
(1)由已知有



所以

(2)




所以

即


而



知识点
由等式









(1)试求数列

(2)若甲数列的每一项都是乙数列的项,且乙数列中至少有一项不是甲数列的项,则称甲数列是乙数列的真子数列.试证明:数列

正确答案
见解析
解析
(1)解:由


由

(2)即对任意的



这表明对任意的




而对于










知识点
数列{an}是公差不为0的等差数列,且a1,a3,a7为等比数列{bn}的连续三项,则数列{bn}的公比为( )
正确答案
解析
设数列{an}的公差为d(d≠0),由a32=a1a7得(a1+2d)2=a1(a1+6d)⇒a1=2d,
故
故选 C。
知识点
已知数列{an}是等差数列,a3=5,a5=9.数列{bn}的前n项和为Sn,且
(1)求数列{an}和{bn}的通项公式;
(2)若cn=an•bn,求数列{cn}的前n项和 Tn。
正确答案
见解析。
解析
(1)法一:设数列的公差为d
由题意可得
解得a1=1,d=2
∴an=1+2(n﹣1)=2n﹣1
法二:设数列的公差是d
∴
∴an=a5+2(n﹣5)=9+2n﹣10=2n﹣1
∵
当n=1时,
∴b1=
当n≥2时,bn=sn﹣sn﹣1=
=
∴
∴数列{bn}是以

∴bn=
(2)cn=an•bn=
∴


两式相减可得,
=
=
知识点
已知数列


(1)求常数

(2)若抽去数列



(3) 在(2)的条件下,试求数列


正确答案
见解析
解析
(1)解:由


又因为存在常数

则


故数列

此时


(2)解:由等比数列的性质得:
(i)当

(ii) 当

所以
(3)解:注意到





(i)当

(ii)当

即
知识点
数列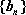
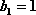

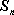

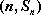
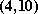
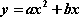
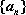
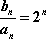
(1)求证:数列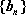
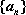
(2)令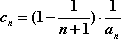
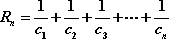
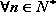

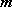
正确答案
见解析。
解析
(1)证明:∵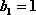
∴点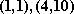
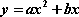
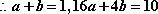
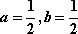
∴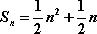
则
∴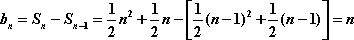
又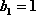
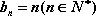
∴数列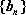
又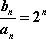
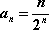
(2)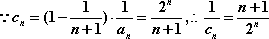
∴
∴
两式相减,得:
∵
知识点
扫码查看完整答案与解析