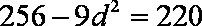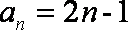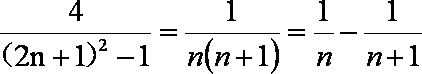- 数列
- 共2062题
已知矩阵

(3,1)变为点(1,1),求实数a,k的值。
正确答案
见解析。
解析
设特征向量为
则 
因为k≠0,所以a=2.
因为


所以2+k=3,解得 k=1。
综上,a=2,k=1.
知识点
如图,












(1)写出





(2)求证:

(3)设



正确答案
见解析
解析
(1)依题意,有

(2)证明:①当

②假设当

则当

得
即
解得

即当
综上所述,对所有

(3)

因为函数






由题意,有
所以,
知识点
已知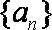
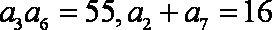
(1)求数列
(2)令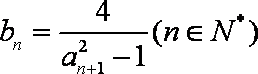
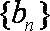
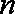
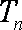
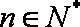

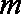
正确答案
见解析
解析
(1)设等差数列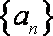
由a2+a7=16.得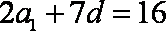
由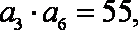
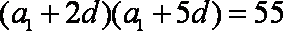
由①得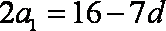
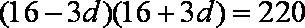
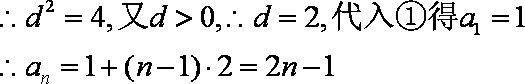
(2)由(1)得
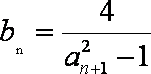


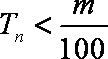
知识点
已知等比数列

(1) 求通项
(2) 若




正确答案
见解析。
解析
(1)

于是
(2)由
又因为
所以数列


于是
因为

解得
经过估算,得到
知识点
已知公差不为零的等差数列

(1)求数列
(2)若



正确答案
见解析。
解析
(1)






所以数列

(2)
所以
=
=
所以
知识点
在等差数列{an}中,若a3+a5+a7=9,则其前9项和S9的值为 。
正确答案
27
解析
在等差数列{an}中,若a3+a5+a7=9,故有 3a5 =9,a5 =3。
则其前9项和S9=
故答案为 27,
知识点
若数列{an}是首项为6﹣12t,公差为6的等差数列;数列{bn}的前n项和为Sn=3n﹣t。
(1)求数列{an}和{bn}的通项公式;
(2)若数列{bn}是等比数列,试证明:对于任意的n(n∈N,n≥1),均存在正整数Cn,使得bn+1=a
(3)设数列{dn}满足dn=an•bn,且{dn}中不存在这样的项dt,使得“dk<dk﹣1与dk<dk+1”同时成立(其中k≥2,k∈N*),试求实数t的取值范围。
正确答案
见解析
解析
解:(1)∵{an}是首项为6﹣12t,公差为6的等差数列,
∴an=(6﹣12t)+(n﹣1)×6=6n﹣12t
而数列{bn}的前n项和为Sn=3n﹣t,所以
当n≥2时,bn=(3n﹣1)﹣(3n﹣1﹣1)=2•3n﹣1,
又∵b1=S1=3﹣t,
∴
(2)∵数列{bn}是等比数列,∴b1=3﹣t=2•31﹣1=2,解之得t=1,
因此,bn=2•3n﹣1,且an=6n﹣12
对任意的n(n∈N,n≥1),由于bn+1=2•3n=6•3n﹣1=6(3n﹣1+2)﹣12,
令cn=3n﹣1+2∈N*,则
数列数列{cn}的前n项和为:Tn=2n+


(3)根据(1)的结论,得
由于当n≥2时,dn+1﹣dn=4(n+1﹣2t)•3n+1﹣4(n﹣2t)•3n=8[n﹣(2t﹣
因此,可得
①若2t﹣

∴当n≥2时,{dn}是递增数列,结合题意得d1<d2,
即6(3﹣t)(1﹣2t)≤36(2﹣2t),解之得

②若2

∴结合题意得d2=d3,4(2t﹣2)×32=4(2t﹣3)×33,解之得t=
③若m




则当2≤n≤m时,{dn}是递减数列,当n≥m+1时,{dn}是递增数列,
结合题意,得dm=dm+1,即4(2t﹣m)×3m=4(2t﹣m﹣1)×3m+1,解之得t=
综上所述,t的取值范围是


知识点
已知等差数列






(1)求数列
(2)记

(3)求数列


正确答案
见解析
解析
(1)因为






又当


当


所以数列


所以
(2)由(1)知
所以
所以
(3)因为
则

由①-②,得
整理,得
知识点
记

…
可以推测
正确答案
解析
本题考查归纳推理问题.根据各式的规律,显然




知识点
己知数列

(1)若

(2)设






(3)若数列











正确答案
见解析。
解析
(1)证明:







(2)由题意得:














(3)证明:设
不妨设


若

若




若












知识点
设等差数列{an}的前n项和为Sn,若a1=﹣3,ak+1=
正确答案
13
解析
∵等差数列{an}的前n项和为Sn,
a1=﹣3,ak+1=
∴Sk+1=


解得k=13。
知识点
设等比数列



正确答案
解析
因为数列






知识点
设各项均为正数的数列{an}的前n项和为Sn,已知a1=1,且(Sn+1+λ)an=(Sn+1)an+1对一切n∈N*都成立。
(1)若λ=1,求数列{an}的通项公式;
(2)求λ的值,使数列{an}是等差数列。
正确答案
见解析。
解析
(1)若λ=1,则(Sn+1+1)an=(Sn+1)an+1,a1=S1=1。
又∵数列{an}的各项均为正数,∴

∴





化简,得Sn+1+1=2an+1,①
∴当n≥2时,Sn+1=2an,②
②﹣①,得an+1=2an,∴
∵当n=1时,a2=2,∴n=1时上式也成立,
∴数列{an}是首项为1,公比为2的等比数列,an=2n﹣1(n∈N*),
(2)令n=1,得a2=λ+1。
令n=2,得a3=(λ+1)2,
要使数列{an}是等差数列,必须有2a2=a1+a3,解得λ=0
当λ=0时,Sn+1an=(Sn+1)an+1,且a2=a1=1。
当n≥2时,Sn+1(Sn﹣Sn﹣1)=(Sn+1)(Sn+1﹣Sn),
整理,得

从而





化简,得Sn+1=Sn+1,
∴an+1=1.
综上所述,an=1,
∴λ=0时,数列{an}是等差数列。
知识点
在等比数列


正确答案
解析
∵数列






知识点
已知在递增等差数列











正确答案
见解析
解析
(1)


设等差数列



当


(2)
=

知识点
扫码查看完整答案与解析